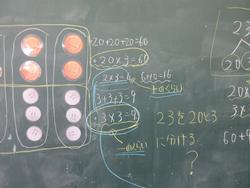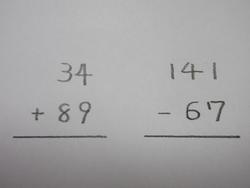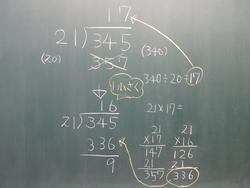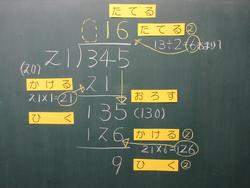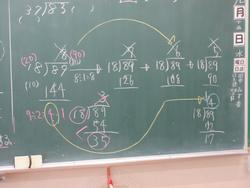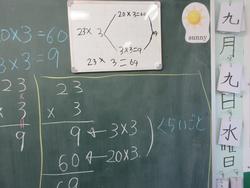算数コーナー
3月17日(木)
卒業式が終わると来週にはいよいよ修了式となります。先生方も通知票作りに大変な時期ですが、先週までにほぼテストは終えているクラスが多いようです。2年生も3月後半の単元のテストを1枚残してもうすべて終わっています。今学期のまとめテストは3学期のまとめテストではなく、1年間のまとめテストとなります。ですから、1学期の学習も範囲になります。
2年生のテスト結果を見てみますと、前回2月16日でお伝えした2年生の弱点(①たし算の筆算の次に来るひき算の筆算をたし算で計算をしてしまう、という問題をよく見ない弱点と②文章題でかけ算の立式をする場合、式が逆になってしまう弱点)がどうだったかがわかります。

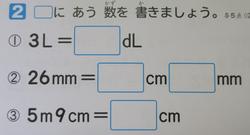
最初の筆算は③をたしてしまう子が今まではいましたが、今回は0人。素晴らしいです。弱点克服とみたいのですが、どうでしょう。間違いは7人でそのうち3人が41です。これは一の位の計算が2-3ではなく、3-2をしてしまうありがちなミスです。この4問は誤答が①3人②0人③7人④3人と優秀です。次の単位換算は誤答が①18人②6人③28人と苦戦しています。①は14人が300dL③は23人が59㎝でした。1L=10dL、1m=100㎝が基本です。単位換算の問題はしばらくやっていないと忘れてしまいます。ここで確認ができていれば1ヶ月後はもっとできているはずです。


この文章題が弱点の2つ目。式の間違え20人中15人が5×8と逆でした。このパターンの間違えは1回目16人、2回目26人、3回目15人となっています。次がどうなるか。今回は文章題が5問出ていて、他の4問の式の間違いは0人、0人、3人、6人なので2年生の文章問題の中でいかにこの4⃣番のかけ算の立式が難しいのかがわかります。この問題のパターンは今後3年生以上で小数、分数も絡めてずっと出てきますので、あと一週間でもう一押ししたいと思います。最後の時計の問題は、問題をよく見ないパターンの問題です。文をよく読まない子は午前午後をつけないで時間だけで答えを書きます。これが①8人②7人いました。午前午後をつければもちろん正解でした。
2月25日(金)
最後は6年生です。6年生の新しい学習は2学期で終わります。3学期は今までの総復習となります。今回の2学期の復習テストは平均が80点を超えよく理解できていました。その中でも気になった問題を取り上げます。
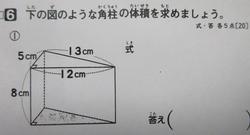
正答率は69%です。体積は底面積×高さでよくわかっていますが、底面積の三角形の面積がどの辺を使うか、また、2でわることを忘れたなどで間違いが目立ちました。


この2問に共通しているのは、数値をきちんと使わないことです。問題文の数値を使うことが基本になりますので⑦は8×1/5000=40000、40000㎝=400m、⑪では30÷15=2、270÷2=135(別回答270÷30=9、15×9=135)となるのですが、⑦では8×5000、⑪では270÷2などとなぜ5000や2が出てくるのかを省いてしまって原点になっています。もちろん考え方は合っていて、答えを出すだけの問題なら大丈夫なのですが、小学校の段階では必要になります。
また、⑦では5000×8(20人)、1/5000×8(7人)と逆にかけている式が目立ちました。これは式の意味が違うので誤答になります。
以上1~6年生まで間違いの多い問題を取り上げてきましたが、自分の学年より下の学年の問題もお子さんに出してみてください。忘れている場合も多いので復習になると思います。また、あまりできていない場合はeライブラリーでその単元の問題にチャレンジさせてください。
2月24日(木)
今回は5年生です。

上の問題は正答率が72%と47%です。こんなに違う理由は1つ。②は答えを約分するのです。11人が約分を忘れています。これができていればほぼ同じになります。ただ70%ほどと考えるともう少し練習が必要です。今の6年生も約分には苦労していました。
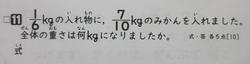

同じことは⑪でも言えます。式の正答率83%に対して正答率は43%。10人が約分忘れです。難しい約分は仕方のないことですが、2や3で割れる数はなんとかしたい。一の位が偶数(例:26と30)なら2で、各位の和が3の倍数(例18と45)なら3で、一の位が0か5なら5で、とパターンがありますので慣れてほしいです。
立式の難しさは⑫です。これもかけ算の意味になりますので、80×50が正解です。50×80は意味が違うので正解にはなりません。ただし、答えは逆でも同じなので答えが合っていれば答えは○としました。はじめの数字50を先に50×80とした子が12人、80÷50とした子が10人いました。また、答え方も一工夫が必要です。80×50=4000ですが、なぜか答えは4㎏です。わかっているからでしょうが、ここは4000g=4㎏または4000÷1000=4という式が必要になります。2点減点しました。
高学年の約分忘れや中学年の0の消し忘れはもったいないですね。何度か失敗すると覚えるのかもしれませんが、やはり忘れていく方が多いです。たまに振り返りができるとよいです。
2月21日(月)PART2
今回は3、4年生です。


最初のひき算の筆算は、単純に2ですが、小数第一位の0を消さなければなりません。2.0と書いた子が間違いの30人中23人で正答率は43%。これこそ忘れてしまった、うっかりしたというミスですが、ちょっと多いですね。次の文章問題は2年生と同じで、式を逆に5×280と書いた子が間違いの20人中13人で正答率は62%。逆の式にした子が2年生が半数近くでしたが、3年生では25%ほどということは学年が上がるにつれ、わかってくるということでしょうか。

こちらの文章題は間違えの23人中9人がたし算(300g+1㎏100g)でした。文を読むとたし算のような問題ですが、実はひき算という問題です。ちょうど2年生が図をかきながら学習しているところです。「ミカンを7個食べたら残りが6個でした。最初に何個あったでしょう。」のように残りならひき算と1年で学習したのに、たし算で計算するという問題です。


続いて4年生です。最初は計算のきまりの問題です。教科書では「分配のきまり」と書いてあります。×45が同じなので、(13-6)をしたあとに45をかけるのですが、この扱いは少なく、しかもあまり使わないところなのでどうしても忘れてしまいます。正答率は15%で間違いの多くは585と45を入れていました。気持ちはわかります。円の面積で×3.14を使う時に知っていてほしいきまりです。次は4年生最大の課題「2けたでわるわり算」です。正答率は66%から51%です。計算間違いではなくやり方がわからなく手を付けない子が8人~13人います。なんとかしないとということで、この計算が必要な小数の単元で個別指導も取り入れて、学年を3つのクラスに分けて学習することにしました。計画通りなら今日からスタートでしたが学年閉鎖で少し遅れてのスタートです。


この文章題は計算のきまりを使った問題です。間違いの28人中10人が60×5-1000としています。考えはほぼ合っていますが、-1000がひけないのに答えは正解の700と書いています。もう少しです。ここでも数字が出てくる順番に式を作っていると思います。最後は27人中16人が6000と書いています。百の位までの概数という場合は百の位の下の十の位を四捨五入します。百の位を四捨五入なら6000ですが、百の位までの概数ですから5800になります。やり方を忘れたか勘違いしたかという問題です。
ここの問題はぜひもう一度お子さんに少しずつ挑戦させてください。
2月16日(水)PART1
前回お知らせした一斉テストの結果が出ましたので紹介します。
まずは1年生です。

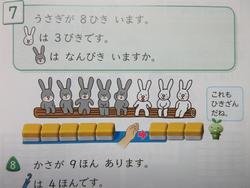
1年生はどの問題もとてもよくできていました。ただこの問題だけは難しかったようです。どちらがいくつ多いの問題は立式だけでなく、答えの書き方も難しいのです。式は74%、答は47%の正答率です。答えは「8わ」とだけ書いた子が15人もいました。正解は「すずめが8わおおい」になります。
続いて2年生です。


2年生ではちょっとした実験(2年生は問題をよく読まない。)をしました。筆算の問題ですが、普通はたし算が先に出てくるパターンが多いのです。そのときに2番目の問題がひき算にもかかわらず、たし算をしてしまう子が必ず数名います。そこで今回はひき算を先に持ってきました。結果はなんと正答率①88%②68%です。しかも②の間違え15人の内11人がひき算で計算していました。もちろんこの11人はひき算だったら正解(407)です。実験結果は私の予想通り、式をよく見ないで計算しているということの証明になったのではないでしょうか。計算でこの結果ですから文章問題だとなおさらです。問題文をよく読んで、見直しをして、とよく言いますが、なかなかこのミスは減りません。学年が上がるとともに減ってくるので、それに期待するしかないのでしょうか。「問題をよく読んでね。」は2年生への口癖にもなっています。
もう一問は文章題です。子どもたちはどの学年でも数字が出てくる順番に式を作る子が多くいます。この問題も同じで7×4とした子が26人(12月のテストではできていた子10人含む)いました。4×7も7×4も答えは28なんだからよいのでは、と思いがちですが、式を立てる場合は式の意味が重要になってきますので、かけ算の場合は(一つ分の数)×(いくつ分)=(全部の数)で立式をします。これは6年生になっても影響してきますので、今後も復習を続け、2年生で確実にさせたいと思っています。式の順番が違うだけなので、答えがあっている場合は答えは○(77%)としました。
1月31日(月)
先週から各学年で3学期一斉テストを行っています。これは2学期も行いましたが、12月に行われた2学期のまとめテストの中から約7,8割の問題を抽出し、テストをしてから1か月後にもう一度やって定着度を見るものです。


テストの丸付けとともに、誤答の分析をし、再度児童に定着を図っていきたいと思います。わかりましたら、このコーナーでお知らせしますので、家庭学習に役立ててください。特に不得意なところがわかればeライブラリーの活用で基礎力アップが図れます。
1月6日(木)
ついに6年生の順番が来てしまいました。ちょっと大変です。いや、かなり大変です。5年生の問題は全部で10問です。ですから忘れてしまうのはある程度仕方のないことです。と前振りをして、

③だけどうしたのでしょう。アを18人、イを9人が選んでいます。逆に考えてしまったのでしょうか。
 ①31%②70%です。
①31%②70%です。
①は100倍して10倍したのですから全部で1000倍、だから1000でわれば元に戻ります。ウを選んだ子が24人です。
②はわられる数を100倍すれば、わる数も100倍しないとダメなのですが、イを選んだ子が10人です。
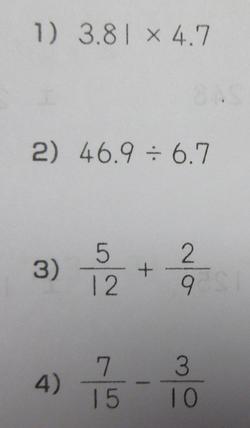 ①63%②77%③33%④30%です。
①63%②77%③33%④30%です。
①②も大変ですが、問題は③④です。6年生で分数のかけ算わり算をがんばったためでしょうか。分数のたし算わり算をかけわり風に解いてしまったのです。たしひきの基本は通分して分母を同じにして、たしひきします。かけわりは約分をしながら分母同士、分子同士をかけます。それでどのように計算したかというと、③の場合は12と2を約分、12と9を約分、これが9人、そして12+9、5+2とたし算、これが17人です。④も同様で順に8人、18人です。素直な6年生ですから、かけわりを学習して頭がかけわりのやり方になってしまったかもしれません。もしかしたら不注意でかけわりの問題と勘違いしてやったのかもしれません。いずれにしても、半分どころか3人に2人が間違ってしまったのですから、もう一度確認する必要があります。3学期が始まってすぐに校長問題として再度挑戦です。これを読んだ子どもたちは分数のたしひきを再度確認してください。一度確認すれば思い出すはずです。
1月5日(水)
いよいよ明後日から3学期は始まります。そろそろ宿題をやっていなくて焦る頃でしょうか。それとももう終わって余裕でしょうか。今日からは前回に解説をした1学期復習テストの翌週に行った前学年の計算の基礎問題10問のテスト解説をします。習ったときは覚えているのですが、しばらくすると悲しいことに忘れてしまいます。これは多かれ少なかれ誰にでもあることです。その部分をはっきりさせ、適度に復習をすることでより深い理解につながると考えます。そのための1つの分析です。
まずは取り上げた問題をお子さんに出してみてください。一緒に考えてもいいですね。ちょっと心配と思ったらeライブラリーでその学年の単元に戻って問題を解いたり、解説を見たりすることができます。
1年生はありません。まずは2年生です。1年生の問題ということになります。

2年生は前半の6問は97%という素晴らしい正答率です。残りの4問は文章題の式と答えが2問ずつです。ここの正答率が78~85%と不得意なところです。上の(1)は問題文に数字が3つあるのもポイントです。文章を理解して数字を選ぶ必要があります。違う数字を選ぶ子が5人、また、かけ算の学習のあとということで6×5とした子が4人いました。
次は3年生です。
 正答率は69%です。
正答率は69%です。
午後3時を選んだ子が6人、2つに丸を付けた子が5人です。時計はデジタルに慣れてしまっているのが原因ですが、学校ではほぼアナログを見ているはずです。あとは問題をしっかり読めば、と思うのですがどうでしょう。
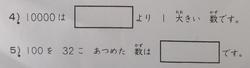 ④は77% ⑤は73%です。
④は77% ⑤は73%です。
よく出てくる数を相対的に見る問題で1年生から4年生まで数が大きくなりながら出てくる問題です。
④は1000とする子が5人で999が2人です。⑤は320とする子がほとんどで10人です。0の数をきちんと見ていないのでしょうか。たぶん10を32こ集めた数という問題でも320と答えると思います。
かけ算九九の問題も4問出ていましたが、こちらは6×7だけが10人間違え、答えを48とする子が4人でした。他の3問の間違えの合計が7人なので、6×7だけ異常に間違えているということになります。6×7、6×8、4×7は鬼門です。
次は4年生です。
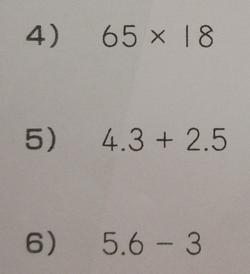
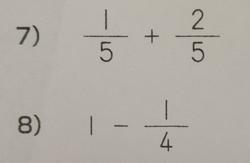
間違えの多かった問題の正答率は②76%④58%⑥75%⑧45%となります。
②は80÷9で答えの8はよいのですが、あまりの間違えがたくさんありました。④は23人の間違えの答えがほぼバラバラでした。計算ミス、位取りのミスが多いと考えられます。⑥は5.3とした子が7人、これも位取りのミスです。それとも不注意でしょうか。⑦は87%正解と素晴らしいのですが⑧のように1が出ると急にできなくなります。誤答で1/3が7人いるのですが、分母の4から1を引いたのでしょうか。1を4/4と見ることができればよいのですが、忘れているようです。
次は5年生です。
 正答率は68%で、イを選んだ子が16人います。よく見れば正解すると思うのですが。これも3年生の問題と同じで数を相対的に見る問題です。4年生になると億兆が出てきますのでまずは丁寧に数えることが大切です。読み方も含めて0があると間違いが多くなります。
正答率は68%で、イを選んだ子が16人います。よく見れば正解すると思うのですが。これも3年生の問題と同じで数を相対的に見る問題です。4年生になると億兆が出てきますのでまずは丁寧に数えることが大切です。読み方も含めて0があると間違いが多くなります。
次は計算です。
 正答率は②66%③84%④69%です。
正答率は②66%③84%④69%です。
4年生の④と同じように数が大きくなったかけ算やわり算(かける数わる数が2けた)は①やり方を忘れる。②途中の計算ミスが多くなる。③小数点の位置のミスという理由で正答率が下がります。特に④は正解の140.4に対して1404が3人、14.04が2人、1.404が1人となっていました。
6年生は次回にします。自分の学年だけではなく、下の学年の問題にも挑戦をさせてみてください。算数は積み重ねですので間違えている場合はどの学年の内容でつまづいているのかがわかると復習もしやすくなります。昔の教科書はなくてもeライブラリーならば丁寧な解説と豊富な問題があります。ぜひ活用を。
12月28日(火)
今回は1学期復習テストの分析の最終回6年生です。6年生は8月4日にここでお知らせした内容とかなり似ていますので、8月4日のコメントを参照しながら見ていただければと思います。
まずは基本的な計算問題6問で④~⑥までは前回お知らせしましたが、この全6問の平均正答率が約90%から84%と約6%落ちています。特に⑥は88%から78%に下がってしまいました。少しずつ忘れていると考えるしかありません。
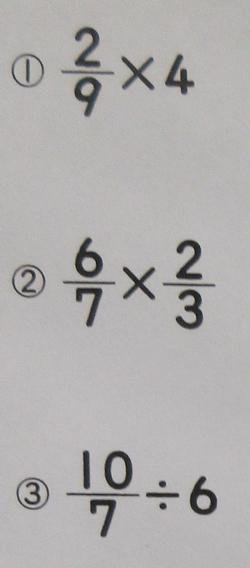

文章題が難しいのはいつの時代もどの学年も同じなのですが、8月4日に⑩、⑪を取り上げて説明をしました。


8月4日の⑩が上左の4⃣、⑪が上右の7⃣になります。さらに、6⃣
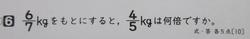 を追加します。
を追加します。
この2問はそれぞれ⑩75%→71%、⑪44%→42%と若干下がっています。さらに6⃣も61%→55%と下がっています。4⃣の正答率は6⃣、7⃣と比べるとずっと高くなっています。(70%以上)なぜでしょう。4⃣と6⃣、7⃣の違いは式が数値が出ている順番になるかどうかです。4⃣はそのまま1 3/4×2/3で正解となるのです。誤答の10人は1 3/4÷2/3となってわり算にしてしまいました。6⃣、7⃣は数値が出てくる順番と逆の式になるので、その分、誤答が増えると考えられます。6⃣の正解は4/5÷6/7ですが、6/7÷4/5と出てくる順番に立式した子が19人います。7⃣の正解は3/8÷2/3ですが、逆の2/3÷3/8にした子が11人、かけ算にした子が15人いました。
この文章題も簡単な数にして、6⃣「2㎏をもとにして6㎏は何倍ですか。」と考えれば6÷2と答える子が増えると思います。同様に7⃣も「2dLのペンキで4㎡ぬれる。」とすれば4÷2と式は出ます。あとは数値を変えればよいのですが、「簡単にするっていうけど、どう簡単にするの。」と言われそうです。このあたりがきっと難しいのだと思います。授業では図をかいたり、数直線や表をかいて、丁寧に意味の学習をして答えを求めたのですが、テストで出てくると、そういうやり方(図、表など)をして解く子はほぼいないので余計難しくなります。
12月27日(月)2
6年生の1学期復習テストの分析は明日お知らせしますが、6年生がこのテストの翌週に行った前学年の10問テストで大変な事実が明らかになりました。この事実は最終週に6年生に直接指導したかったのですが、時間がとれずできませんでした。年を越す前に是非とも6年生には確認をしてほしい問題です。
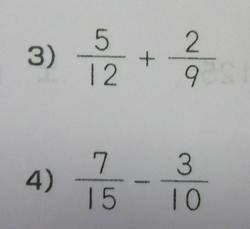 これは5年生の2学期の内容です。
これは5年生の2学期の内容です。
5年生では2学期に通分や約分を学習し、分母が違う分数のたし算ひき算を学習します。そして6年生では分数のかけ算わり算を学習します。かけ算わり算をしっかりやると5年生のこのたし算ひき算を忘れてしまうのです。どうするかというと、パターンは2つ。
1つは③の場合12+9、5+2をして7/21、これはかけ算わり算だと分母同士分子同士をかけわりをするのですが、たしひきは通分をしないといけません。36で通分して15/36+8/36=23/36ですね。
もう一つはどこでも約分をしてしまうのです。④の場合は3と15を1と5、または15と10を3と2、かけわりなら3と15を約分しますが、たしひきは答えが約分できたら約分するだけです。④は通分して14/30-9/30=5/30で約分して1/6ですね。正解者はなんと57人中③は19人、④は17人正答率はそれぞれ33%、30%になります。特にたしひきをした子は17,8人もいます。たぶん忘れているだけなので、早く思い出すためにもまずはこの問題を解き直して、さらにeライブラリーで復習してほしいです。
12月27日(月)
クリスマスが終わりました。子どもたちはどのように過ごしたのでしょう。テレビでのプレゼントをもらう瞬間のビデオなどを見ていると例年と変わらない楽しい様子が見られます。ただ、プレゼントがとても高価なものになっているような気もします。次はお正月に向けての準備になりますね。子どもたちもおうちのお手伝いがしっかりとできるとよいのですが。
さて、算数は5年生の問題です。
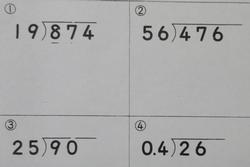 小数が出てくるわり算です。
小数が出てくるわり算です。
ここは本当に難しいのです。4年生で難しかった2桁でわるわり算に小数も入ってきます。ただ、答えを見ていると2桁でわる方はなんとかなっていますが、小数点の位置に苦しんでいます。②は85の答えが9月は17人でしたが今回は6人に減りました。③も17人から8人と①~③は正答率が上昇していますが、なぜか④だけは6.5、0.65が21人正答率が60→40%と落ちています。わる数が小数の場合を忘れているようです。
 計算の工夫です。
計算の工夫です。
工夫しなくても答えがあっていればよいのですが、工夫しない場合計算が複雑で計算ミスをしています。②は3.7と6.3をたしてから1.2をかければ、10×1.2で暗算でもできるのですが、ここは正答率前回50%から今回62%とよくなっていますが、まだまだ不十分です。①は4×2.5を先に計算して10なのでここも暗算で96となります。
 4つから2つ選ぶ問題です。
4つから2つ選ぶ問題です。
ほとんどの子はアは選ぶのですが、もう一つをウにしてしまう子が約20人です。4÷3なら1.33‥なのでこちらを選んでも良さそうなのですが、0.09に惑わされます。ウは100倍して、400÷9ですから44.44‥ですね。

最後はお決まりの文章題です。小数が入るのでなんだかわからなくなります。これが2mの棒が6㎏だったら、きっとできると思います。正答率は式が60%、答えが40%です。式はできても計算ミスをする子が20%ほどいるということになります。式は簡単な整数にして考えてみるとわかることが多いです。
5年生の結果は全体でみると9月とほぼ同じであまり忘れていないということになります。あとはできていないところをさらに復習してほしいです。特に小数の計算での小数点の位置です。
12月24日(金)
先週でしょうか。クイズ番組でクリスマスイブはクリスマスの前の日か当日の夕方かという問題で出ていました。今まで当然のように前の日と思っていて、ついでにイブイブは前々日と思っていたのに違っていました。調べてみたら、なるほどそういうことかと思いました。さらに25日はイエスキリストの誕生日でもなかったのです。何十年も思っていたことが違っていました。そんなこともありますね。
さて、今回は4年生です。
 このパターンは2年生から続いている問題です。
このパターンは2年生から続いている問題です。
算数の言葉では「相対的に見る」と言われていますが、2年で3桁、3年で千万・億までとだんだん数が大きくなって4年生で完成します。この6問の平均は9月83%から今回76%に下がっています。特に2⃣②は67%で50000万と書く子が5人です。気持ちはよくわかりますが、大きな単位は普段使わないので忘れてしまいます。苦手な場合は前の学年から復習するとよいです。
 わり算は正答率が上がっています。
わり算は正答率が上がっています。
ただ、4問の平均は9月の70%から今回の75%なので、もう少しがんばらないといけません。これは2学期に2桁でわるわり算の学習をしたため、1桁でわるわり算の復習になったと考えられます。特に④は63%です。数が大きくなってあまりが出ると間違いも多くなります。
 苦手な文章題は答えがポイントです。
苦手な文章題は答えがポイントです。
この種の問題はあまりをどのように答えとして書くかも問題です。そのままあまりを書くこの問題のパターンはよいのですが、あまりを切り捨てたり、切り上げたりするので問題をよく読むことが大切です。答えの書き方は9月の57%から63%に上がりました。
4年生で一番の難関の2桁でわるわり算の復習とともに、まずは1桁でわるわり算を確実なものにしてほしいと思います。
12月23日(木)
前回の続きで3年生です。
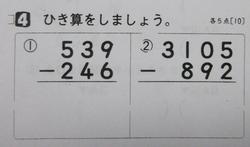 繰り下がりのある筆算です。
繰り下がりのある筆算です。
9月に84%71%できていた問題が72%56%に落ちています。平気で①313②3793と、下からひいてしまいます。一度確認すると思い出すのですが、その記憶がいつまで持つかが問題です。できればずっと忘れないでほしいのですが。
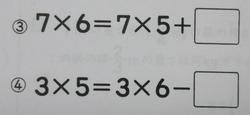 ちょうど2年生のテスト問題です。
ちょうど2年生のテスト問題です。
9月に両方とも90%近かった正答率が、75%ほどになっています。
 時間と時刻です。
時間と時刻です。
9月とあまり変わらないのですが、75%前後で不得意なことに変わりありません。忘れるというよりは生活なので、日常的に使っている子は忘れません。
という結果です。かけ算、わり算、たし算の基本は大丈夫です。上の3種類をeライブラリーで復習すると、忘れていた記憶がよみがえると思います。
12月20日(月)
この12月に2つのテストを全校一斉にやっています。1つは1学期のまとめテストからの抽出問題、もう一つは前の学年の復習問題です。いずれも問題数は少なめで計算問題が中心のテストです。これは前に学習したことをどれくらい覚えているかの確認テストです。忘れやすいところは冬休みの宿題でもあるeライブラリーで学習してくれることを期待しています。
1学期のまとめテストは、9月にも行いました。そしてこの12月です。この2回のテストを比べて、各学年のだんだん忘れている問題を紹介しますので、冬休みの学習の参考にしてください。
まずは1,2年生です。
 これは1年生です。
これは1年生です。
1年生の問題はぜんぶで16問ですが、この式と答えの間違いの総数が他の14問の間違いの総数とほぼ同じです。つまり、ここがポイントです。2つ合わせて9月の計30人の間違えに比べると23人と減りましたが、正答率80%にまだ届きません。また、式が書けなかった子(無答)がたくさんいたのですが、8+6という間違いが多くなりました。これは大きな前進です。あと一歩です。たしざんかひきざんかということと、ひく場合はどちらからひくかということ、この2点を文章題から図が想像できて、式にできるとよいです。他の問題の正答率が95%を超えていますので、文章題と2学期の復習を冬休みの課題としてください。
次は2年生です。


1⃣は繰り下がりのあるひき算です。式は6人→1人、答えは16人から9人とよくなっています。正答率も80%を超えました。式が立てられればあとは計算です。このパターンは筆算をしないで解く子の間違いが目立ちました。筆算で計算すると7⃣の上の③や7⃣の②のパターンのように繰り下がりのミスが少し減って、今回は2つとも正答率85%以上で正答率が上がります。あともう少しです。
1学期の内容をかなり理解しているので2年生は1学期の復習よりは2学期の復習に力を入れた方がよいです。特にかけ算九九の暗唱やかけ算の文章題でどちらがかけられる数(1つ分の数)なのか文章から読み取ること、あたりです。
2年生はかけ算九九が冬休みの課題となっています。たくさん聞いてあげてください。
12月16日(木)
前回に引き続き2年生です。かけ算の学習がほぼ終わり、テストも行いました。まだ九九については十分ではありませんので学習カードを使って、聞き合いなど取り組みも毎日のようにしています。一般的には6,7,8の段が難しいとされていますが、今回のテストでは8×8が63、4×9が63など、答えが1違いの間違いと十の位と一の位が逆という間違いの2パターンが目立ちました。この後も練習は続けます。ご家庭でも練習の成果を聞いてあげてください。つっかえてしまったときはすぐ教えてあげて、また最初からスタートがオススメです。


12月7日(火)
2年生はどちらのクラスもほぼかけ算の学習が1~9の段まで学習を終えました。同時に九九を覚えることも行っていますが、これには練習量の差や個人差がかなりあります。この後はかけ算の九九表を使ったきまり見つけや、かけ算を使った発展問題などに取り組んでいきます。もちろん九九を覚えることも平行して行いますが、今後は今まで以上におうちの方の協力が必要になってきます。1つの段を唱えるのは約10秒ほどです。学校でも友達同士の聞き合いや先生の聞き取り、学習カードを使った学習などをしていますので、ぜひご家庭でも今まで以上に聞いてあげてください。
はじめに学習した2の段、5の段、その次の3,4の段まではよいのですが、どうしても、6,7,8の段は苦手な子が多いです。というよりもまだ練習不足です。学校では2学期中に何とか言えるようにして、冬休みはすらすら言えるように時間も計りながら、そして、3学期に完璧となるようにしていきます。日常生活の中のちょっとした時間に、九九練習を取り入れてください。忘れていたら教えてあげてください。この時期が人生で一番九九を練習する時期です。
12月1日(水)
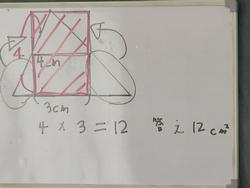
5年生の先週の授業からです。面積の授業です。最初は平行四辺形の面積を学習します。私たちはとにかく公式と考えがちですが、授業ではまず考え方を重視した授業から始めます。今まで学習した正方形と長方形の面積から平行四辺形の面積(この場合は平行四辺形を長方形に変えて面積を出し、公式を作ります。)を考えます。

この写真は三角形ですが、すでに学習した長方形や平行四辺形の面積に変えて三角形の面積を出しています。左は三角形を2つ重ねて平行四辺形にしています。右は三角形を切り取って移動して長方形にしています。このように習った形にすれば、今までの方法でできる。と学習していきます。そして、公式も覚えるのですが、まずは全員で作り出します。左は平行四辺形の公式の底辺×高さから三角形を2つ使ったので2でわって、三角形の面積の底辺×高さ÷2を作り出します。右は底辺を半分にしているので底辺÷2×高さから底辺×高さ÷2となります。
最終的には公式を覚えて面積を出すことになるのですが、こういう考え方を学習することで、次の学習に活かす考え方が身につくと言われています。
11月16日(火)
これは11月の上旬の授業です。1年生はたしざんで繰り上がりがある計算とひきざんで繰り下がりのある計算に取り組んでいます。今回は繰り下がりのあるひきざんの最初でした。今までは9-8や16-4など繰り下がりがなく、一の位でひけばよかったのですが、この時間は13-9という式で3-9ができないのでどうしようという学習でした。
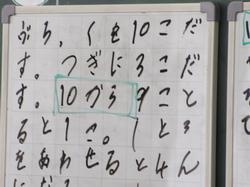
子どもたちは言葉や式、特にブロックを使って、3から9(ばらひくばら)はひけないので、10のまとまりからばらの9をひく、と考えました。10から9をひいて1、ばらの3とあわせて4と答えを出しました。指をおって答えを出す子にとっては13は指が足りないので困ってしまいます。でも10からひくなら大丈夫です。あとは早く慣れて、指を使わなくてもできるとよいです。子どもたちにとってはひきざんなのに、ひいてたす、という操作がつまずきの1つにもなっています。
この学習を理解したあとに、もうひとつのやりかた、ひいてひく、も学習します。13-9なら13-3-6です。これもまた子どもたちが戸惑うことになるのです(同じ式なのにやり方が2つある。)が、いずれも図を使ってどのようにひくのか考え方を確かめながら学習しますが、初めのうちは苦戦します。練習問題を解きながら、自分でどちらが計算しやすいかわかるとよいです。ここでしっかり学習をするのですが、2年生になると、2桁の計算になり、3-9はひけないので9-3で6となってしまう子が結構います。一度確認すると思い出す子が多いです。
10月13日(水)
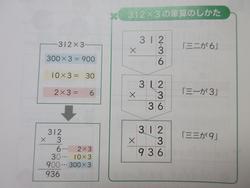
2年生と4年生の筆算をお伝えしてきましたが、3年生も筆算の授業がこの時期にありました。3年生は初めてのかけ算の筆算です。2年生までにたし算とひき算の筆算は学習しています。そしてかけ算九九を学び、3年生で九九よりも大きいかけ算の学習になります。筆算はこういうやり方だよ。と教えるのではなく、どうしてこういう形になったのかを学習します。つまりみんなで筆算を作るのです。
授業では23×3をまずは図を使ったり、式を分けたりしながら答えを出します。答えがわかったあと、筆算の形を考えます。
するとたし算やひき算の時と同じように考えるとおかしいところが出てきて、かけ算の筆算はかける数をかけられる数の一の位と十の位にかけることを、図や式で学習したことから見つけ出します。
23×3は20×3と3×3を合わせた数で筆算でも同じ計算をしていることを見つけました。


筆算ができるようになると、次は繰り上がりがある問題、かける数が3桁の問題と進んでいきますが、これらは基本のやり方を知っていればできると学習し、筆算の習熟に入っていきます。どの学年も同じですが、繰り上がりやたし算でミスがあったり、数字を小さく書いて見間違えたり、という間違えと0が入ってくると位がおかしくなる間違えが多くあります。練習問題をたくさん解いて、筆算に慣れてほしいです。
10月11日(月)
少し間が開いてしまいました。2年生も4年生も筆算の学習が終盤に入っています。
2年生は桁数が増えて、3桁のたしざんとひきざんの筆算です。たしざんの場合は答えが3桁になるため、繰り上がりが2回出てきます。ひきざんは3桁から2桁をひきますので、繰り下がりを2回することになります。さらに102-16のように一の位がひけないから十の位から繰り下げるけど、十の位もないから百の位から1繰り下げて、十の位に10、その10から1繰り下げて十の位が9で、一の位に10となる。この10と2で、一の位の計算は12-6=6(または、10-6+2=6)、十の位の計算は9-1で8となり、答えは86。というように説明をするとこんなに長くなる筆算を説明もできるように学習しています。
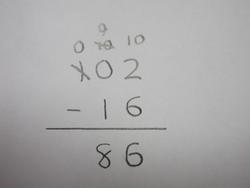
右の2問はご家庭でできるかどうかチェックを。
4年生のわり算の筆算は前回9月22日にお知らせしたように3桁÷2桁の計算が最大の難関です。ポイントは仮の商を立てることと、その仮の商をどの位に立てるかということです。つい百の位の上に仮の商をたててしまうと、思い込みがあるのでスムーズに進むのですが、実は間違っているということになります。
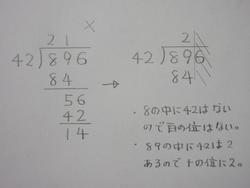
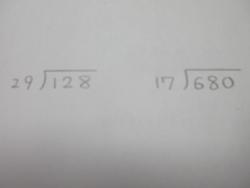
右の2問はご家庭でできるかどうかチェックを。
その他には計算のきまりでわる数とわられる数を同じ数でかけてもわっても商は変わらないということを学んだので、8000÷700など数が大きくなる計算も出てきます。この場合は両方を100でわって80÷7と同じになります。ただやっかいなことはあまりです。80÷7なら11あまり3ですが、8000÷700だと11あまり300になります。商は11と変わらないのですが、あまりは変わるのです。ここが間違いやすいポイントです。
9月22日(水)
前回から一週間が過ぎ、4年生のわり算はいよいよ商が2けたになる難関へと進んできました。式は345÷21です。昨日までは同じような問題で153÷24を150と20にして、15÷2=7から考えていましたが、今日は同じようにすると340÷20で34÷2=17となり、ここでノートが止まってしまう子がたくさんいたのです。考えを発表する場面で、この先を同じように計算して、答えを出せることがわかりましたが、21×17、21×16の計算が大変だというのです。

そこで他の考えで計算した考えを聞くと、1学期に学習した72÷3と同じやり方をしていたのです。72÷3を教科書を開いて確認し、前のくらいから1つずつ見て、①3の中に21はないから0だけど書かない。②次に34の中に21は1個だから1あとは「たてる」「かける」「ひく」「おろす」の手順で計算していたことを思い出しました。この通りに計算すると簡単な計算で答えが出ることがわかりました。数が大きくなって難しいと思っていた計算も実は今までにやったやり方でできることがわかりました。あとは問題を解いて、この計算の仕方に慣れることが大切になってきます。何しろこのわり算を1つ解くために、かけ算とひき算を少なくても4回しています。かけ算ミス、繰り下がりミスをしないでやっと答えが出るのです。大変な作業です。

(写真はわかりやすいように授業の板書を真似て見やすく書き直しています。)
9月15日(水)
4年生の「2けたでわるわり算」の学習です。今まで「かりの商」を立てて計算することを学習してきましたが、昨日今日はこの「かりの商」が合わなかったときの学習です。「かりの商」というだけあって、とりあえずの答えなのです。ですから違う場合もあります。ただ、今までの学習でそんな操作はありませんでした。ここがつまずきのポイントです。
写真を見ると89÷18を80÷10と考え、8÷1=8で8をかりの商とすると、計算が合わなくなってしまいます。(89-144でひく数が大きくなってひけない。)そのため、かりの商を1小さくして計算するとうまくできたというのが昨日でした。今日の場合は5回目(かりの商が8→7→6→5→4)にやっとできたということになります。こんな面倒なことをやらないとだめなのか、とみんなに考えを聞くと89は90,18は20と考えれば90÷20は9÷2で4が一発で出る。という意見が出ました。かりの商の出し方を工夫すれば、正解に早くたどり着けるとまとめましたが、これが一発でうまくいかない場合もあります。そこは練習問題で慣れていくことになります。そして、さらにこのあとわられる数が3けたになり、商が2けたになり、とより難しい計算がやって来ます。ですからこのあたりの基本をしっかりと身につけさせていきたいと思います。
9月13日(月)
前回の続きになります。6年生の分析です。
6年生は分数の計算はほぼできているのに、やはり文章題の立式に苦労しています。8/4付けの記事での10番11番の問題はそのまま出題したのですが、かけ算かわり算か、またはどちらが前に来るかで悩んでいます。7月上旬に一度テストして、その答え合わせもしたはずなのですが、2ヶ月後の9月1週に実施した同じ問題でも間違いは多くありました。今回の正答率は10番が75.4%、11番が43.9%、他にもう一問「6/7㎏をもとにすると4/5㎏は何倍ですか。」の立式は61.4%でした。この問題も整数で考えると、2㎏をもとにすると6㎏は何倍と考えると、6÷2=3となるので、実際には数字を入れ替えて4/5÷6/7と考えやすくなるのではないでしょうか。また、「もとにする」というキーワードで、もとにする数でわることを知っていれば÷6/7ができますね。
9月7日(火)
先週どのクラス(2年生以上)も算数の1学期のまとめテストの問題を中心にテストを行いました。採点をして、1学期の学習を覚えているかどうかの確認をしました。分析をしていますので、結果は少しずつお知らせします。
まずは4年生です。8月6日の記事でも書きましたが、2けたでわるわり算の学習に入ります。これは、1学期の1けたでわるわり算ができていないとできません。それがわかっていても難しい単元になります。まずはわり算の筆算をほぼ忘れてしまった子どもたちに個別指導で思い出してもらい、次に全体で復習してから、本単元に入ろうと考えています。この学習の様子はまたお知らせします。
8月10日(火)
今回は1,2年生です。ただ、1年生はたし算、ひき算の学習が終わったところで、1学期のまとめのテストもありませんでした。たし算とひき算はよくできていました。2学期に繰り上がり、繰り下がりが出てくるのでそこがポイントになりそうです。合わせて10のパターンが指を使って、(両手を開いて10,そこから数えて6を折って、残りを数えて4)ではなく、反射的に、例えば10は6と…、4。10は8と…2など出るように日頃からクイズのように出していくとよいと思います。
2年生
2年生の1学期の学習内容は①グラフとひょう②たし算のひっ算③ひき算のひっ算④長さのたんい⑤3けたの数です。まとめテストではひっ算が気になりました。

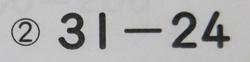
まず、最初の筆算ですが、学習しているときはほぼ間違えないのですが、時がたち、久しぶりに解くと、間違えがどっと増えます。一の位の計算を8-6としてしまうのです。6-8はできないので十の位から1繰り下げて、となるはずですが、52と答えた子がとても多かったです。次の問題は横の式を筆算にして解く問題です。これも同様の間違えがありますが、さらにプラスして、問題の写し間違い、ひき算なのにたし算をしてしまう、というミスもあります。わかっているので一度やると思い出すのですが、久々は要注意です。

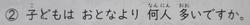
上の問題文は①では合わせて何人ですか?なのでよくできていました。②はひき算だとわかるのですが、数字を問題に出てくる順番に26-34とかき、平然と答えを8とするパターンと34-26まではよいのですが、横式のまま計算すると12という答えがたくさん出てきます。これは最初の2問と同じ理由です。
2年生では定期的に少しずつ計算問題をやって慣れていくことが大切ではないでしょうか。これは先に説明した3年生でも同じことが起こっています。
8月6日(金)
前回は5,6年生のお話をしました。今回は3,4年生です。
4年生
4年生の1学期の学習内容は①大きい数の仕組み②折れ線グラフと表③わり算の筆算(1)わる数が1けたです。まとめテストでは5種類の問題が気になりました。まずは一番大切なといってもよいわり算です。ここでは大きな数を1けたの数でわるのですが、3年生の時のように1回ではわれません。3⃣①②のように答えが百の位からなのか十の位からなのか、見通しを持つことから始まります。これがやっかいなのです。見通しが持てればあとはかけ算九九でOKです。ただ、ひいたり、かけ算九九をしたりするのでミスも目立ちます。そして2学期は最大の山場の「わる数が2けたのわり算」になります。この学習までに1けたでわるわり算は完璧にしておきたいです。


次の5⃣は間違いが多いのが少し意外でした。分度器の当て方が学習したばかりで慣れていなかったのかもしれません。慣れればなんてことはないのですが、角の中心と分度器の中心をしっかりそろえるとこがポイントです。ものさしを学習した2年生もそうですが、0をそろえるというのが慣れるまでは大変なのです。
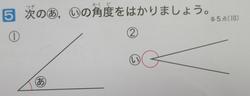
最後はやはり文章題です。1⃣は式はできています。ポイントは筆算での計算ミスです。420×137の筆算では全部で9回のかけ算と9回のたし算があります。これをミスなく計算するのですから大変です。
3⃣はわり算のあまりをどうするかの問題です。素直に割り切れればよいのですが、あまりが出るときは3パターン考える必要があります。1つめはそのままあまりを書く。答えは77箱あまり1こです。2つめは3⃣でいうと、「全部箱に入れるには箱は何箱必要ですか。」これはあまりも箱に入れるので箱は78箱必要です。3つめは「箱は何箱できますか。」これはあまりは聞いていないので答えは77箱になります。これらを問題文で読み取り、答えを出します。


eライブラリーでは「わり算の筆算(1)わる数が1けた」、「角の大きさ」になります。
3年生
3年生の1学期の学習内容は①かけ算②時刻と時間③わり算④たし算とひき算の筆算⑤長さ⑥あまりのあるわり算です。まとめのテストでは7種類の問題が気になりました。まずは慣れると何でもないのですが、普段あまり使わない考え方の時刻と時間です。問題には時計や数直線でヒントがあるのですが、間違えてしまいます。まずは時刻は何時何分、時間は何時間何分、または何分間を表すという意味がわかることが重要です。時計や数直線をかいて考えるとわかりやすくなります。

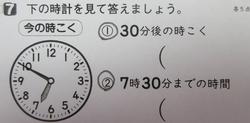
時間の繰り上がり繰り下がりもあまり使わないので間違えが多い問題です。生活のほとんどは10進法です。それに対して時間は60進法なので60で1繰り上がります。同様に1m=100㎝=1000mm、1L=10dL=1000mL=1000ccなども忘れがちです。2年生で説明しますが、かさの学習で10dLや100mLの量の感覚をつかむために具体物をたくさん用意し、体験しましたが、子どもたちにとっては難しかったようです。かさや重さ、長さなどは量の感覚(量感)をつかむことが一番大切です。大人でも、この荷物何キロぐらいとか、ここからあそこまで何mぐらいというのは少し難しいですね。
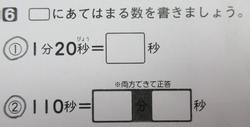
繰り上がり・繰り下がりのある筆算はほとんどが計算ミスによるものですが、下から上をひいてしまうミスもたくさんあります。1年生で初めて繰り上がり繰り下がりを学び、2年生では2けた、3年生では3けたと進んでいきます。繰り下げた数字はいくつになるのか、どこに繰り下げたのかをきちんと書いておかないと、自分の書いた数字がわからなくなってしまいます。また、4⃣①の十の位の計算では3から4は引けないから、百の位から1繰り下げて10、10と3で13から4をひいて9、もしくは10から4をひいて6、6と3をたして9、とすればよいのですが、たまに3から4はひけないので4から3をひいて1、とやってしまう子もたくさんいます。これが上に最初に書いた下から上をひくミスです。

9⃣の文章問題は簡単なわり算の立式ですから24÷4となるのですが、その下の②のような形で問題が出ると、なぜか1÷8、8÷1と書いてしまうのです。問題を読んで理解すれば24÷8となるのですが、問題を適当に読むと、出ている数字の1と8だけでだけで、考えてしまうのです。


最後にかけ算のきまりになります。これは2年生でも学習しています。7×6の答えは7×5に7をたした数、逆に3×5は3×6から3をひいた数という、かけられる数をたしたりひいたりすると、かけ算九九の答えはわかるという問題です。もうひとつきまりがあって、かける数とかけられる数を変えても答えは同じというきまりです。これはよくできていました。例えば2×8=8×□という問題です。
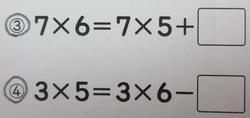
3年生のこれらの問題は、やってみると思い出すのですが、久しぶりにやるとワルレテイルというパターンが多いので集中して一気に学習するよりも、間をおいて一週間に一度学習するなどがよいと思います。
eライブラリーでは「時こくと時間の求め方」、「3けたの数のたし算」、「3けたの数のひき算」になります。
8月4日(水)
現在各担任の先生方とともに、算数テスト1学期まとめの簡単な分析を行っています。全体的な傾向をつかみ、不十分な箇所をこの夏休みにeライブラリーで重点的に補習できればと思います。
6年生
1学期は主に①対称な図形②文字と式③分数のかけ算④分数のわり算⑤分数の倍が学習内容です。まとめのテストではこの5問です。まずは分数同士のわり算です。やり方としてはわる数を逆数にしてかけることが基本です。あとは帯分数の整数部分を分数にすること、約分をしっかりすることです。間違いの多くは、わかっているのに計算ミスをしたり、約分はできたけどもう少し約分できるのにしていなかったり、ということが多いです。
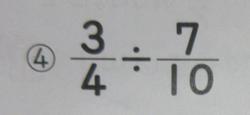
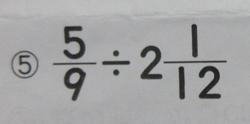
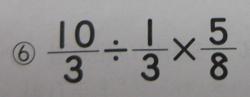
上の問題は通知表の観点で言うと知識・技能に当たる問題です。下の問題は思考・判断・表現に当たる問題です。


この問題は分数になった途端にできなくなる問題です。どちらが前に来るかわからないのです。例えば⑩が1mの重さが3㎏でこれが2mの重さは、とあれば3×2と式ができるのです。あとは数字を入れ替えれば式はできます。分数の場合は簡単な整数にして式を考えると、3,4年生の問題となり、解きやすくなります。同様に⑪も2dLのペンキで3㎡ぬれます。1dLでは何㎡、とあれば3÷2と式ができます。あとは数字を入れ替えて、3/8÷2/3となります。1年生でも何年生でも、出てくる数字を順番に並べて式を作る子がいます。意味を考えれば式の順番が見えてくるのですが、そこまで考えないで式を作ってしまう場合も多いのです。
この単元の復習はeライブラリーでは「分数のかけ算」、「分数のわり算」になります。
5年生
1学期は主に①整数と小数②直方体の体積③比例④小数のかけ算⑤小数のわり算⑥小数の倍が学習内容です。6年生と比べると小数か分数の違いで内容が似ていますね。まとめのテストではこの4問です。
111111
① 1.9)8.74 ※ 少し見づらいです。
111111
② 5.6)4.76
小数のわり算の基本はわる数を整数にするために小数点の移動をすることです。
111.1
①ならば10倍して 19)87.4 にします。答えの小数点の位置も重要です。
111.1
②のパターンは 56)47.6 となり、計算して
.85
56)47.6
44 80
2 80
2 80
0 となり、答えの .の前の0を忘れてしまう問題です。
この2問は知識・技能になります。そして、下の2問は思考・判断・表現の問題です。6年生と比べると小数か整数の違いで問題もよく似ています。ですから6年生と同じように考えて、簡単な整数の問題として考えられれば、3,4年生の問題になるのです。


⑧は 1Lの重さが2㎏のはちみつ3Lの重さと考えると、式は 2×3になります。数字を戻せば1.4×2.7となります。
⑨は 2mの重さが3㎏の鉄の棒で1mの重さはと考えると、式は 3÷2になります。数字を戻せば1.23÷1.5となります。これも6年生の⑪の問題と一緒で、何も考えずに数字が出てくる順に式を作ると間違えてしまいます。簡単な数にすることで、式がわかることが多いのです。
5、6年生の問題で見ましたが、この方法だけで全員ができるわけではありません。やはり、思考・判断・表現というだけあって、文の意味を考え、何算かを判断し、数値を吟味し、式に表現するという力が問われます。ただそれはもとをたぐれば、1~4年生で学習した+-×÷の問題と同じなのです。
この単元はeライブラリーでは「小数のかけ算」「小数のわり算」「どんな計算になるのかな」になります。つまづいている場合はeライブラリーでいくつか前の学年に戻って学習することも必要かと思います。eライブラリーには問題に対して詳しい解説がついていることも大きな魅力です。
8月3日(火)
eライブラリーでの話の続きになります。
算数に限らず学校で教える内容は学習指導要領にもとづいています。そこでは算数の内容は4つに分けられています。A 数と計算 B 図形 C 測定 D データの活用 です。小学校の算数といえば「かけ算九九」とよく言われますが、このかけ算は A 数と計算 の領域です。この領域は特に系統性が強く前の学年の学習内容がとても大切です。1年生で学んだたし算とひき算、そして、繰り上がりと繰り下がりは4年生の大きな数の計算まで使います。さらに、このたし算の考え方で2年生のかけ算の意味の学習を行います。その後かけ算九九は暗記して覚えることになりますが、3年生のわり算はこのかけ算から答えを出します。最後に4年生での最難関の2桁でわるわり算(252÷18)では、4年生前半で学習する概数の考え方、繰り下がり、ひき算、かけ算を使います。また、5,6年生では3,4年生で学習した小数や分数を四則計算できるようにします。これらももとをたどれば1~4年生までの計算ということになります。私がよく言うのは、「100+200も0.1+0.2も1/5+2/5も全部1年生の1+2だよ。」です。もとの考え方は同じになります。
長々と書きましたが、つまり、前の学年の内容がわかっていないと今の学習ができないということです。これはいくらわり算の筆算の計算の仕方を説明しても、概数やかけ算、繰り下がり、ひき算の考え方が不十分だと、その場はやり方がわかったと思っても根本が理解されていないので、次の日にはまたわからなくなってしまうというパターンです。もちろんやり方をしっかり覚えて、どんどんできるようになる子もいます。実際に我々の世代の頃はあまり意味を考えずにやり方だけで来たような気がします。なぜ、円の面積は半径×半径×3.14なのか、台形の面積は(上底+下底)×高さ÷2なのか、なぜ分数のわり算はわる数を反対にしてかけるのかなど。
話がそれてしまいましたが、習った学習は少しずつ忘れていくものです。それを少しでも忘れないように時々前に戻って学習をするとよいと思います。スパイラル学習などと呼ばれることもあります。そのためにeライブラリーはとても有効だと考えます。eライブラリーを進めていくと種から芽が出て、葉が出て、大きく成長していきます。この木も是非育ててください。どう育っていくのかは私もわかりません。子どもたちに見せてもらっています。
7月21日(水)
終業式の話の一部です。7月の校長先生問題のまとめをしました。まずはたして80になる筆算です。これは4年生まで対象を広げたところ、3,4年生も頑張ってくれました。最高記録は3年生の14個でした。たして2021になる筆算は、6年生が45個考えてくれました。2021問題は少し難しかったようです。
80を例に説明をしました。まずは筆算の秘密として、一の位の繰り上がりがあるので、十の位はたして7、一の位はたして10、これが基本です。ですから十の位は1と6,2と5,3と4のペアになります。そして、一の位は1と9,2と8,3と7,4と6になります。後は同じ数字にならないようにするのですが、例えば十の位が1と6,一の位が2と8とすると、12+68ができます。ここで2つめの秘密として1パターン見つけると、数字の場所を変えることでいくつかできるのです。この場合なら
12 18 62 68
+68 +62 +18 +12
と上の4つができます。1つのペアができると4つできますので、合計はいくつになるでしょう。
2021問題も同じです。45個見つけた6年生は1パターンで45個見つけました。パターンはもう少しありますので、全部見つけると、こちらは200個以上になります。先生方も挑戦してくれて、3パターン発見した先生もいました。また、4年生でこの数字は絶対使わないと発見した子もいました。素晴らしい発想です。全部見つけるやり方は6年生の最後の方で出てきますので、説明はここまでです。夏休みにもう少し頑張ったら2学期に教えてくださいといいましたが、余裕があればご家庭でも考えてみてください。粘り強く考えた子どもたちに拍手です。
7月6日(火)
昨日の昼の放送です。「校長先生もんだいの途中経過です。高学年問題は惜しい人が1人、正解者なし、低学年問題は最高が7つです。高学年特に6年生は頑張ってください。また、低学年問題は4年生までと変更します。3,4年生も挑戦してください。」というような内容でした。
高学年用 1~4年生用

1年生にとっては繰り上がりも習っていないので難しい問題でごめんなさいなのです。
いずれも0~9のカードを1枚ずつ使って筆算の答えを出します。正解は1つではなく、たくさんあります。一つ見つけるとその仲間がたくさんあるのですが、そのあたりに気づけるとよいと思うのですが。是非ご家庭でもお子さんと一緒に考え、ヒントをあげてください。締め切りはまだまだ先です。
6月25日(金)
これは先週17日の授業です。先週お話ししましたが、実習生の精錬授業です。3桁+3桁で答えが500になる筆算を探すという授業で、探すためには何か秘密がある、それを授業で探していきます。

授業では秘密を探し出すことができて、授業も終わったのですが、授業の後に校長から「では500になる式はどのくらいあるんだろうね。」という問題を投げかけ、「興味のある人はおうちでやって、校長室までノートを見せに来てください。」といいました。取り組んでくれた子は数人なのですが、このように興味を持って、おうちで何かしら取り組んでくれるとうれしくなりますね。算数に限らず、学校で気になったことをおうちの人に聞いたり、ネットで調べたり、ということができるようになってほしいです。
今回は隣のクラスもこのクラスの前の日に同じ授業をやっているので、少し遅くなりましたが、「隣のクラスでこういうことにチャレンジしています。最高は18個です。興味のある人はおうちでチャレンジしてください。」と話をしました。
答えはまだまだたくさんありますので、これを読まれた3年生の家庭では是非チャレンジをお願いします。本当はこれにも秘密があるので授業で秘密発見の授業もできそうです。
6月10日(木)
2年生の長さの学習から、竹ものさしを紹介します。竹ものさしのは長さを測る側と線を引く側があります。
目盛りのある方で線を引くとだんだん目盛りが見えなくなってきます。

授業では2つに苦労しています。1つは長さをきちんと測りとること。もう一つは点と点にものさしを合わせて真っ直ぐな線を引くことです。ですから、間違っている子は直接引き方を見て、正しい方法を教えています。ちょうど1㎝全部少ないという子や点に鉛筆が当てられない、引いているうちにものさしがずれてしまうなどうまくいかない理由がわかってきました。長さの計算も特訓中ですが、どれも毎日少しずつ取り組んでなれてほしいと思います。家庭でも線を引く、長さを読む練習やeライブラリーでの練習に取り組ませてください。
さて、話題を変えて、ものさしの溝の話です。この溝は現在ではまず使いませんが、元は毛筆で線を引くときに、墨がものさしにつかないようにするための補助の棒が通る溝です。下の写真のようにペンに割り箸を添えて固定して、割り箸を溝に沿ってまっすぐに動かせばペンはものさしを汚さずにまっすぐな線が引けるということです。最近はプラスチックの1m定規にペンをそのままつけて線を引いてもインクがにじまないように定規の端に角度がついていますね。いろいろな工夫がされていますが、竹ものさしは今も変わらず昔のままのようです。
6月4日(金)
校長先生問題2つめの答えを2日の給食中に発表しました。正解は10人です。6年生が5人、4年生は一人でした。前回より3人正解が増えました。6年生が本気を出したのかもしれません。お見事です。
さて、これを図でかきますと、
前 ○○○○○○○○○○ 後ろ
1234567松
高54321 となります。16人の時との違いは 高 と 松 の位置が変わっていますね。
この並び方でも松本君は前から8番目、高橋さんは後ろから6番目、そして2人の間には2人います。見方を変えると違った答えが出てくることもあるのです。
この放送のあと校長室の前にいると、「校長先生、4年生の一人って誰ですか。」「教えないよ。」「だいたいわかるな。」「誰なの。」「○○くん。」「なんで、そう思うの。」「だって、隣のクラスだけど頭いいもん。」という会話をしました。
5月13日(水)
今日放送で校長先生問題の答え16人と正解者の人数、そして、ともうひとつある答えの正解者が3名であること、さらに、もう一つの答えをあと一週間考えてみましょうといいました。校長室前の問題にはヒントも追加しました。放送後には何人かがすぐやってきて、「先生、わたしのこたえあってたよ。」(1年生)、「これわかる?」(6年生)など声が聞こえてきました。

5月12日(火)
5月の全校朝会で子どもたちに出した校長先生問題です。校長室の前に2週間ほど貼ってあります。休み時間や帰りの時間になるとときどき「これわかった?」「1つはわかるよね。」などの声が聞こえてきます。それでも答えを出してくれた子どもたちは前回より少なくなりました。ちょっと難しかったでしょうか。
子どもが1列にきちんと並んでいます。松本君は前から8番目です。高橋さんは後ろから6番目です。
そして、松本君と高橋さんの間には2人子どもがいます。
さて、子どもは全員で何人いるでしょう。
1、2年生の皆さんは答えを1つ見つければ正解です。
でも3年生以上の皆さんはきっと答えを2つ以上見つけられるでしょう。(2年生ももう1つ見つけられるかな)
1年生で学習する問題ですので2年生以上は答えが1つは出せます。1年生はうまく考えて出せるとよいです。ただ、これでは楽しくありませんので、少しひねってみました。答えはもう一つあるのです。見方を変えなければなりません。図をかくと、少し見えるかもしれません。今日がしめきりでした。集まった回答は28枚です。ほとんどは1つ目の答えは正解です。学習していない1年生も5人が正解です。すばらしい。
前 ○○○○○○○○○○○○○○○○ 後ろ 図ではこのようになり答えは16人
1234567松12高54321
そして、2つ目の答えを見つけた人は4年生1名、6年生2名でした。図もよく書けていました。とてもすばらしいです。
なお、このことは明日放送で伝え、答えは2つ以上とかきましたが、もう一つあることも伝え、2つめの答えのヒントを出して、もう少し考えてもらおうと思っています。
4月20日(火)
5年生の「直方体や立方体の体積」の学習です。面積も同じように学習しているのですが、どうしても学習していくうちに数の計算ばかりで基本を忘れがちです。面積も体積も基本は1㎠、または1㎝3(PCで文字が出ないため3を小さく下に書きました。)がいくつあるかということでそれぞれの大きさを表しています。例えば、縦2㎝横3㎝の長方形の面積ならば、2×3=6ですが、実は一辺が1㎝の正方形1㎠がいくつあるかと考えるのが基本です。ですから、図では、
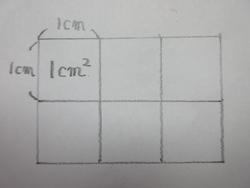
1㎠の正方形が、縦に2個、横に3個あり、2×3=6 で6個、1㎠が6個で6㎠となります。
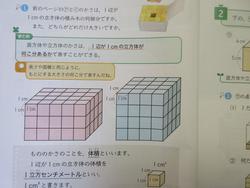
これを5年生の直方体に当てはめると、1辺が1㎝の立方体(サイコロ)1㎝3 が何こあるかで立方体の体積がわかるということになります。
授業ではすぐ式の計算や公式にいくのではなく、下の図のように1㎝3 の立方体を実際に使い、自分たちで作った立方体や直方体の中に1㎝3が何個入るのかを確かめる学習が大切になります。

教科書でも実際に何個かを表していますが、授業で子どもたちが自らやってみて確かめるという活動によって、より基本の考えが自分のものになると思います。
そして、このたくさんの立方体の数を1こずつ数えるのは大変であり、簡単に求めるにはかけ算が便利だと学習することになり、公式につながっていきます。実際にものを使って、手を動かした学習は子どもたちの理解度も深まると思います。
4月12日(月)
4年生の最初の学習です。考え方というのは何通りかある場合があり、いくつも考えられる児童もいますが、自分の考えで1つわかってしまうとその他の考えが入ってこない場合があります。例えば自分と同じ考えだけど自分は式を使って解いた。違う子は図や表を使って解いた。という場合はわかることもありますが、根本の考え方が違うと理解に苦しむようです。そういう場面は話し合いの中でお互いの考えを理解して、わかっていければ理想的です。

今回の問題は1箱6個入りで24円のガムを18個ではいくらという問題です。ほとんどの子はガム1個分を出してから18個分を出していました。つまり、24÷6=4 4×18=72となります。24÷6=4で1個あたり4円を求めてから全体を求めるという考え方は5年生で学習する「単位量当たりの大きさ」につながる大切な内容です。
少数派ですが、18÷6=3 24×3=72 という式も出ました。この考え方を説明するのに1個を求めた多数派はちょっと困りました。なぜ18÷6をしたのか。私たちは24÷6なのに。これは18個のガムを6個ずつ分けるということで、図をかくとちょっとすっきりしたようで、3は3箱分ということがわかり、1箱分24円なので24×3という式も理解することができました。
式を読むという学習は各学年であり、とても大切な学習です。算数を説明するのに式が一番簡潔に整理された形なのですが、逆に簡潔に整理されたために、その式の意味することがわからなくなってしまう場合があります。ですから、式の意味を図や表や言葉で説明することが大切になってきます。
3月26日(金)
3個と3個が同じなら、残りの2つを比べればわかる。
3個と3個が違うなら軽い3個を見て、1個1個で比べ、軽い方があればそれで、同じなら残ったもう1個になります。下の二人の回答は言葉と図で上手に説明をしています。ベストアンサーです。
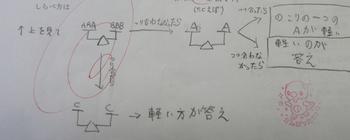

頭の中で判断して諦めるのではなく、実際にやってみると、あっそうか、とわかる場合もあります。算数の世界ではハンズオンまたはハンズオンマスという言葉で呼ばれることもあります。
来年度も子どもたちへいろいろな場面で算数問題を出していきたいと思います。
3月25日(水)
下の問題、答えはズバリ2回です。児童で説明の十分な正解者は7名でした。
比べ方は①1こずつのせる。②2こずつのせる。③4こずつのせる。では答えは3回か4回になってしまいます。そこで前に答えは3,4会ではないと話したので、「えっ、それじゃあ2回なの。」「そうです、答えは2回です。」となり、1,2,4こずつでは、だめだということは、3こずつのせるということになります。「3こずつだと残りが2個でできない。」となりますので、「確かめないうちからできないと思わずにまず3個と3個に分けてみよう。で、3個と3個が同じ場合次どうするか、3個と3個が違った場合次度どうするかを考えてみよう。」で答えの説明ができないでしょうか。
明日子どもたちの丁寧な説明を載せます。
3月22日(月)
前回から3週間がたっているんですね。先週答えを出してくれた人には丸付けをして返却しましたが、見事な正解者は7人いました。もう少し説明が欲しい、答えはあっているという子も何人かいました。ただ正解者はいずれも5年生以上でした。私としては、まずこの長い問題を読んで理解し、答えが出せることが大切だと思います。答えが違っていてもいいのです。今回の問題は自分なりにやってみればとりあえず答えは3回または4回と出ます。答えが出たという達成感を味わうことができます。
そして、その答えが違うとわかってさてどうするか、もうひと踏ん張りできるかという問題です。いろいろな場合を想定して考えないと解くことができません。そうなると答えを出せる子は1年生以上ですが、正解となると高学年になってしまうのでしょうか。
子どもたちに配付した問題はこれになります。今度は家庭で皆さんで考えてみてください。教員でも正解にたどりつけない人はたくさんいます。だいたいはあきらめてしまいます。
問題 PDFファイル![]() 正解は二日後に。
正解は二日後に。
2月26日(金)
全校朝会でこの3ヶ月校長先生問題として算数の問題を1問出しています。1年生から6年生までいるのでどんな問題を出すのかが悩みですが、1,2年生にはどうしても少し難しくなってしまいます。それでも、少しは取り組めるようにと考えています。今回も10人ほどがチャレンジしてくれました。
さて、今回の問題ですが、1,2回目と比べて、答えを持ってきてくれる子どもたちがだいぶ増えました。1回目は約40人、2回目は約20人ですが、今回は2日間で70人ほどです。理由はわかりませんが、1,2回目は全校朝会の話の中で問題を見せて、やる気のある子にプリントを渡していたのですが、今回は校長室前に問題を張るので、興味のある子は来てねと言いました。そのため、休み時間になると問題を見に来たり、問題用紙を取りに来たり、問題の前で友だちと考えたり、もちろん問題を解いて出しにくる子もいます。それらの相乗効果で増えたのかもしれません。
そして、70ほど集まった答えを見ると、今までは90%以上の正答率がなんと全員残念な結果に。2人だけ数はあっていたけれど、考え方が書いていなかったので、正解にはなりませんでした。
ということで、26日の給食の最後に放送をしました。①たくさんの子がやってくれてありがとう。②正解が一人もいない。③ヒントはほとんどの人が書いた答えの3回は違う。という3点です。放送後の校長室前はまた子どもたちがたくさんやってきて、問題用紙を持っていきました。どんな答えを書いてくれたか、確認してまたお知らせします。
2月19日(金)
1年生の教科書もいよいよラストに向かっています。こんな単元があります。

授業では新しい学習をするときに1年生でも6年生でも式だけで文章問題を解決することはまずありません。言葉や図や表やグラフ等を使って、式の意味を考え、図などと対応させながら学習します。
1年生のここでは1⃣で単純な形を学習します。そらさんは前から6番目で、後ろに4人いるのでみんなでは6+4=10で10人になります。図で書いたり、ブロックを置いたりして確かめることができます。
この学習から5時間ほど後に学習するのが9⃣です。久しぶりの並び順の問題です。今度は前に4人、後ろに3人です。教科書はヒントになるので見せませんでした。ポイントはそらさんと前、後ろの人数が図や絵、ブロックなどでできるかということになります。
授業ではまず自分で考えます。式で4+3=7という式がいくつか見られたところで、そらさんの場所を図で確認しました。前4人、そらさん、後ろ3人です。これを式にすると、


左の写真の黒板の右のように、上から3つの式ができました。子どもたちの説明は5+3=8(前の5は前4人とそらさん)も4+4=8(後ろの4はそらさんと後ろ3人)も図を使って、子どもたちにわかりやすくできました。そして、4+3+1(1はそらさん)も説明ができました。
最後には、式は文章題に出てくる数字を使うことを確認し、今回の場合は問題文にはありませんが、そらさんの分の1が式に入ることを図で確認し(写真右)、4+1+3=8という式になることを確認しました。
○○○○ そら ○○○
前4人 +1人 + 後ろ3人
このパターンの問題は、データが古いのですが、10年ほど前の学力テストで全国平均が40%ほどでした。最近では、これに似た問題で49%というデータがあります。図に書けば結構わかるのですが、式だけでやってしまうと勘違いからか、間違えが多くなっていると私は考えます。
2月5日(金)
昨日5年生の授業で面白いなと思ったことがありました。まずは板書を。

という問題で まず2×3.14=6.28 と出ました。すると 「親切な言葉で」と先生から、私は「ん?」でしたが、子どもたちは前にもやったことがあるようで、「そうか」「わかった」と黒板に下の4つの考えが出てきました。
①1×2×3.14 ②(1+1)×3.14 ③1+1=2 2×3.14 ④1×2=2 2×3.14
親切な言葉とは、つまり、問題の数値を使った式、誰が見てもわかりやすい式となるでしょうか、問題文には半径1cmとしか書いてありません。それなのに式でいきなり2が出てきたら、なぜ2?となります。そこでそのなぜ2?になるかの説明を式の中に入れるのです。円周は直径×3.14ですから、まずは半径の1を直径にします。これが①~④では1×2や1+1になっています。そこでどれが正解なのかというと、すべて正解ですが、3年生で直径は半径の2倍と習っていることを考えると①④のように1×2(倍)を使った方がよいことになります。式は1つでも2つでも問題ありません。
文章問題では文に出てくる数値を使って式を立てるのが基本ですが、それを頭の中で計算してしまって、簡単な式で解いてしまう場合があります。わかったうえでやっていることなので、答えは正解ですが、式としては○をもらえないときもあります。そんな時にこの親切な言葉が思い浮かべば、丁寧な式(問題の数値を使った式)が作れると思います。クラスだけに通じる言葉というのは、クラスの団結力を作ります。「○○君の解き方(方法)」で解いてみよう、などと授業中に出た○○君の解き方がすごくわかりやすくて、そのまま「○○君の解き方」だけでクラスにはどんな解き方かがわかるなんていうことがあります。
2月2日(火)
6年生の算数は、2学期末までに新しい学習内容は終えています。3学期の内容は、

P198~P227までがまとめになります。まずは自分で問題を解いて、答え合わせをして、間違えやすい問題については、先生の解説や友だちの説明で確認をしていくのですが、間違ってしまった子は間違えの理由に気付き、次は同じ問題が解けるようになったかの確認が十分にできません。
そこで教科書には何年生で学んだ内容という吹き出しがあります。昔の教科書に戻るのは難しいので(持っていればぜひ見てほしい)、こういうときにeライブラリーを活用してほしいです。例えば上の問題は、今年何回か書いた内容の「数の相対的な見方」についての問題です。問題の横を見ると、4年整数のしくみ、5年小数のしくみと書いてあります。eライブラリーでその学年のその単元を開けば問題がたくさん載っていますので、復習が十分にできます。
6年生のeライブラリーの土日の活用状況は他学年と比べると多くはないので、こういう機会を利用して活用してくれればと思います。

式はA:30÷12=2.5 B:48÷20=2.4 ここまでは良いのですが、どちらが混んでいるのかを求めます。ここで間違ってしまいます。この問題はもう一つ解き方があります。A:12÷30=0.4 B:20÷48=4.166…
1つ目の解き方は2.5と2.4でAの数値が大きい、2つ目はBの数値が大きい。この次が重要で、しかも忘れやすいところです。
大事なのは何をもとにしているかです。1つ目は12人でわっているので人数をもとにしています。一人当たりの面積です。つまり一人当たりなら面積が小さい方が混んでいる。2つ目は30㎡でわっているので面積をもとにしています。1㎡当たり何人いるかです。つまり大きい方が混んでいる。したがってどちらで解いてもBが混んでいるとなります。
ちなみに5年生の学習では①人数を揃える。12と20なので60に合わせると、30×5=150、48×3=144となり、60人当たりの面積が出て、Bが数値が小さいので混んでいる。という方法も考えとして出ています。同様に②面積を揃えると、30と48で240に合わせると12×8=96、20×5=100で240㎡当たりの人数が出て、Bが大きいので混んでいるとなります。この2つの考え方は数が大きくなってしまうので、大変だということで単位量当たりの大きさで求める方がよいと学習しています。
1月15日(金)
3,6年生の5問問題の集計が終わりましたのでお知らせします。
まずは前回からお話している問題で似た問題が3年生でも出ています。③24000は1000を□こ集めた数です。これの正答率はなんと87%で、他の学年では見られなかった高い正答率です。その他で心配なのが①25×5×8で工夫して25×40から25×4=100を使えば暗算で1000と出る問題です。そのまま計算しても125×8で答えは出ます。ところがここが35%、3011-1146は繰り下がりに気を付ける問題ですが、60%、③の7.6-3も60%と位や繰り下がりのミスが多い問題でした。
6年生は計算は90%程度でどれも順調ですが、間違えやすい文章問題2問に苦戦しました。2のカフェオレ問題は全体を3:5で8と見られるかどうか、3の鉄問題では1mを求めるときにどのような式になるかを問う問題です。式も答えも40%を切り、復習というより間違えやすい理由がわかるとよいと思います。
1月4日(月)
24日(木)の問題の4,5年生についてです。
まず4年生の問題は「0.001を350こ集めた数は□です。」この正答率は31%、やはり10人に3人が正解です。間違がえで一番多いのは、0.350で10人、これは小数点以下の最後の数字の0は書かないことを忘れてしまっているので、次回は大丈夫でしょう。2番目以降は、3.5が8人、3.50が5人、3.500が2人でいずれも位を1つ間違えています。
5年の問題は「0.052は52の□倍です。」選択肢は1000倍、100倍、1/100、1/1000です。正答率は54%です。選択肢があった影響で正答率も上がったのかもしれません。1000倍とする子は15人。52の1000倍は52000だから違うのですが、0.052を1000倍と考えてしまったようです。
他の問題を見ると、4年生は似たような問題「3080億を1/10にした数は?」で55%と順調、②の「3+4×7」は86%と素晴らしい正答率です。誤答の49も5人と少ないです。これは6年生の学力テストで6,7割の正答率という計算のきまりを問うひっかけ問題です。算数コーナーの10/5と12/2付の内容の通りで、一度意識すればその次はほぼできるという典型的な問題です。繰り返し学習することで忘れていたポイントを意識できるようになり、正答率も上がってきます。
5年生は「2.3×5.7=23×57÷□」で41%、「3.28×7.5」で48%と分数(④80%⑤68%)に比べ不調でした。5年生は分数が弱いと一ヶ月ちょっと前にわかり、eライブラリーで自主学習を進めてきましたが、分数においてはその成果が出たと考えられます。小数の計算も今後やっていきます。
12月28日(月)
24日(木)の問題ですが、2,4年生の問題を全校集会でも話題として取り上げました。それは「まずは2年生です。10人に7人が間違えてしまう問題です。2年生以上の人は考えてみましょう。」「100を42こ集めた数は?」教室で答えを叫んでもらったので実際はどれくらいわかっているかわかりませんが、2年生の答えは正答率27%でした。間違えをまとめると、間違え40人の中で「142」が12人、「420」が7人、「600」が4人です。142は100と42をたした、420は100倍ではなくて10倍した、600は不明ですが4と2をたして6を600にした?と考えられます。
では1,2年生は集計をしましたので結果をお伝えします。今日集計が終わったので先生方に伝えるよりも早く、ここでお知らせすることになります。
1年生の基本問題①~③はどれも90%程度です。④のさくらんぼ計算は63%、⑤の立式は57%、答えは24%です。特に⑤は3つ数字がある中から2つを選んで式にするのでかなり難易度が高いです。さらに答えは「7こ」とする子が全体の22人で48%、答えはどちらがなんこで答えるので「おにいさんが7こおおい」が正解となり、これも答え方が難しいのです。ただ、間違えやすいと意識して練習をすれば、ほぼ解けるようになるはずです。
2年生は、①~⑥の基本問題が74~96%で6問の平均が85%でまずまずですが、②で+-を間違える子は5人、7×6の間違えが14人で気になるところです。
⑦はほとんどが940(27人)か904(24人)です。1マスをなんでも1と考えてしまいがちです。10目盛りで100ならば1目盛りは10と考えられるとよいです。
⑧は一番上のとおりです。間違えやすい問題がわかったところでその問題を意識して練習できれば次の機会にできるようになっているのではないでしょうか。ぜひそんな問題を教科書などから見つけて、再度チャレンジをしてほしいです。
12月24日(木)
今週は各学年に今学年の計算領域の学習の中から間違えやすい問題を5問程度ピックアップして、校長先生問題として実施をお願いしています。採点・集計・分析は冬休みに行う予定ですが、今回は問題を少し紹介します。
まずは似ている問題が各学年に出ています。例えば、
1年 7は10より□小さい数です。
2年 100を42こ集めた数は□です。
4年 0.001を350こ集めた数は□です。
5年 0.052は52の□倍です。選択肢あり ※ 3,6年は未実施です。
これらの問題は算数の言葉で言うと「数の相対的な大きさ」と言い、ある数を十、百、千または、ある単位のいくつ分に当たるかとみることです。この相対的な見方ができることで、数が大きくなっても小さくなっても結局は1年で学習したことが基本になっているということがわかり、問題も解けることになります。1年で学習した1+2=3は学年が上がり、大きな数では1000+2000、小数では0.1+0.2、分数では1/5+2/5と変わっていきますが、それぞれ1000、0.1、1/5をもとにすればすべて1+2になるのです。子どもたちにとっては苦労する問題です。お子さんの学年より下の学年の問題を聞いてみてください。
12月15日(火) 冬休みの九九学習のススメ
2年生の算数そろそろかけ算の学習の終盤を迎えています。かけ算九九の構成を学習した後は、今まで学習してきた中で見つけたかけ算のきまりをまとめたり、九九表を見てきまりや気づいたことなどを考えていきます。さらに後半は九九を覚えることが一番になりますので、学習カードを利用しながら九九を覚えます。この後の学習(3年生)は九九ができて当たり前の学習になりますので、ぜひ、この冬休みの期間でマスターしてほしいと思います。
そして、子どもたちが家でも九九を唱えると思いますのでたくさん協力してあげてください。例えば1つの段を唱えるだけなら5~10秒ですので、ちょっとした時間を使って、「何の段言ってみて。」と聞くのもいいでしょうし、忙しいときに、九九を聞いてと言われて「後でね。」と言いたくなるところを、「じゃあ1分ね。」などと少しでも聞いてください。私が最後にかかわった2年生はもう15年以上前になりますが、九九表を作って練習して、冬休み後の聞き取りテストでは90%以上が1分以内に2の段から9の段までを一気に言えました。早い子は40秒も切ります。ただし、発音がはっきりしないとOKは出しません。ただ早口だけではだめです。100人ほどの2年生を私の基準で全員聞いて合否を出したのは大変でしたが楽しい思い出です。
子どもたちには登下校時やちょっと外に出るとき、車に乗っているときなど、ほんの少しの時間に意識して、毎日何度も九九を唱えてほしいです。保護者の方には聞いてあげているときに、つまってしまったらすぐ教えてあげてください。思い出すために少し考えさせる、例えば6×8で詰まったら、6の段なら6×7=42に6をたせば次の答えがわかるなど、の方法もありますが、私はリズム優先で「6×8=…」「48だよ、最初からどうぞ。」という感じでした。もちろん何が一番良いかはわかりません。その子の性格にもよるかもしれません。いろいろ試してください。保護者の方と一緒にやることが子どもたちにとっては大きなプラスになると思います。
12月2日(水)
今日は全校朝会がありました。その話の中で算数の話題があり、こんな問題が出
されました。 4年生以上の問題として 2+3×4= を出題しました。
答えは ①9 ②14 ③20 のどれでしょう。
放課後などに担任の先生方に聞いてみると、4年生以上どのクラスも大体できてい
たようです。もしかしたらわからないから静かにしていた人もいるかもしれません。
中には20と大きな声で叫んでしまった子もいるようですが、計算のきまりを使え
ば、3×4から先に計算しますので 2+12で 14になります。
11月30日(月)
27日の6年生の教科書問題は(下の写真)
3/4dlのペンキでは板が2/5㎡ぬれます。1dlでは何㎡ぬれますか。
という問題です。
まず一番は分数なのでかけ算かわり算で迷う問題です。しかもわからないから前
から順にかけたり、わったりしてしまいます。分数でわからないなら、整数で考え
てみるのがよい方法です。もし「2dlのペンキで6㎡の板がぬれる。」だったら、
6÷2=3とわかるのではないでしょうか。そこで数を分数に変えて、同じように
2/5÷3/4と式が立てられれば、何とかなります。
もう一つは1を求める場合はだいたいわり算です。というよりも1つ分(1人、
1dl、1kgなど)を求めるのがわり算です。「6個のあめを2人で分けます。
1人分は何こでしょう。」の場合は1人分を求めるので、6個÷2人となります。同
じようにこの場合は1dlを求めるので、2/5㎡÷3/4dlとなります。1を求める単位
でわっています。この場合はdl。分数が一番の厄介者ですのでまずは整数にして考
えることをおすすめします。
あとは教科書にもあるように数直線で考える場合もあります。最後は分数同士の
かけ算とわり算の計算のしかたですね。 2/5÷3/4=2/5×4/3=8/15 です。
7月あたりに学習しているので6年生は忘れているかもしれません。試してみま
しょう
11月27日(金)
算数の文章問題は苦手な子が多いですね。だいたいは何算になるかで迷います。たまに、文の意味をよく考えずに数字を見て感覚で解いてしまう子もいます。2年生と6年生の問題はよくある問題ですが、間違いが多い問題です。

1年生から今まで「ぜんぶ」はたし算と勉強してきたのに、裏切られる問題です。
たし算なら 15+32=47 だ。簡単。ではなく この数字を見て「47は多い」と気付くとよいのですが。上の写真の(3)のような図がかけると素晴らしいです。
全部で32なので 15+□=32 □を出すには 32-15=17 ですね。2年生3学期の内容なので、3,4年生のお子さんにぜひ試してみてください。
次は6年生の問題です。不得意な子にとってはもう見た瞬間あきらめてしまいます。何算?分数?となるのです。
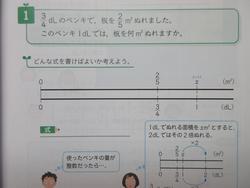
11月24日(火)
2年生でかけ算の学習が進んでいます。あるクラスでは6の段の学習をしていました。授業の最後には3や4の段のかけ算九九の練習もしていました。かけ算の学習はまずかけ算の意味の学習からします。教科書では、2つの意味があります。

と最初に学習しています。教科書のように1台に5人ずつ乗っている乗り物が3台あるので 5×3 としています。まだこの時点ではかけ算九九はわからないので、答えは数えて出します。大変ですが1から順番に数えます。学習が進むとたくさん数えるのは大変だとなり、計算で出したい→たし算で出せる→5+5+5で15となります。それでも7×8となるとたし算でも大変です。
もう一つの意味は倍の考えです。

3㎝が2つ分で3×2、3㎝の2倍が3×2、同じことを言っているようですが、「倍」という言葉を学習します。
どちらも式でかくと3×2になります。
この意味をきちんと理解していないとかけ算九九はできても、文章問題では数値を逆に書いて、間違えとなってしまうことがあります。前にお話ししましたが、算数はまず意味の学習をします。その上で計算練習をたくさんしますので意味の学習が忘れられてしまいます。意味の学習は文章問題の時に重要になってきます。
11月16日(月)
この問題 ① 5/12+2/9 ② 7/15-3/10
「何%ぐらいが正解するか、予想してください。」と書いたまま10日も過ぎてしまいました。
6年生は7月の学力テストでの結果です。①64% ②56% です。
5年生は11月上旬です。学習して1ヶ月ぐらいです。①71% ②43%
習ったばかりと考えると5年生の方ができていてほしいのですが、①はOK、②はまずいです。誤答を見ると、5/30とした約分忘れが7人いて、これが約分して正解だと55%となり、ほぼ同じになるのですが、そう考えると6年生も約分忘れはいるでしょうから、何とも言えません。
ということで前回お話ししたように、約分・通分をこのままにしておくわけにはいかないと考え、eライブラリーを活用して約分・通分にチャレンジしていきます。まずは学校と家庭でeライブラリーを活用して分数のたし算とひき算の問題にチャレンジします。チェック表を作ったところ問題数は約360問あります。内容は24項目あり、それぞれ基本、標準、挑戦問題が5問ずつです。ですからすべて360問やるわけではなく、まずは自分に合ったコースから選ぶとよいと思います。簡単なものからでもよいし、いきなり挑戦問題でも構いません。少しずつやることで力がつくと思います。
eライブラリーの良さは答えの解説があることです。わからなかったら解説を見ます。それでもわからなかったら、先生に学校で聞く。時間をかけて教えてほしい場合は校長室コースも用意してあります。苦手を少しでも減らしていきたいと思います。ご家庭でも声掛けをお願いします。
11月13日(金)
1年生の2回目です。前回のたし算は、①合わせる②増えるという意味の違いでした。意味の違いを学習した後はどちらもたし算として、同じように式を書いて計算します。文章問題では、合わせて、増えると、全部で、来るとなど言葉から判断してたし算の式を作ります。
次はひき算です。ひき算は3通りの意味があります。
①きんぎょが5ひきいます。2ひきとるとのこりはなんひきですか。
②ウサギが8ひきいます。しろうさぎは3ひきいます。こんうさぎはなんひきでしょう。
③赤い花が6ほん。白い花が4ほんあります。どちらがなんほんおおいでしょう。
これらは教科書では、このようになっています。
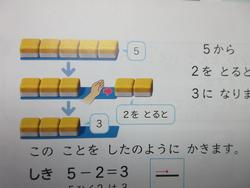
この2つは意味は違いますが、手の操作は同じです。厄介なのは③です。

同じ分を線で結び、残ったほうが残った数だけ多いということになります。この写真の場合は「赤い金魚が2ひき多い」という答えになります。答えの書き方も意地悪で、「2ひき」とだけ書く子がとても多いのです。もちろん問題には「どちらがどれだけ」と書いてあるのですが。
こんな感じでたし算とひき算は意味の学習から入り、どういう場合がたし算かひき算かを判断して、式を作ることになります。ブロックで操作をしながら、意味の学習をするため時間がかかります。でもこれが大切なのです。
11月6日(金)
久しぶりの算数です。今、私が気になっているのが1年生の繰り下がりのあるひき算と5年生の分数のたし算とひき算です。ちょうど今週です。家庭学習を中心に行ってきたeライブラリーを使った復習に7月から取り組んできて、その成果を見てみようということで、10問程度の前学年の復習問題を全校で行いました。結果が揃うまでにはもう少し時間がかかりそうですが、その中で6年生の問題に分数のたし算とひき算があります。
結果からお話ししますと、7月上旬の結果より11月上旬の結果の方がよくなっています。ただしまだ、間違う子が多いのも事実です。復習問題をある程度継続的にeライブラリーで行うことで、改善が見られたことは良い結果でした。この分数のたし算とひき算は5年生の10月に学習します。5年生にまとめテストの結果を聞くとやはり苦手なようです。5年生の段階でもう少しできるようにしたい。これを1つの目標として、5年生担任と協力して、分数のたし算とひき算の基礎基本の定着をねらった取り組みをしていきます。
対象となった問題は① 5/12+2/9 ② 7/15-3/10 です。
この問題5,6年生は何%ぐらいが正解するか、予想してください。
1年生の繰り下がりのあるひき算については今週、来週あたりから入る単元です。今まで繰り下がりのないたし算とひき算、たとえば 4+3 6+4 7-3 10-6 、さらに繰り上がりと繰り下がりがない計算で大きな数として たとえば 13+5 17-4 、そして3つの数のけいさん 7+3+1 13-3-7 を学習し、少し前に繰り上がりのあるたし算(9+4)を学習しました。そしていよいよ繰り下がりのあるひき算となります。
算数はとりあえずは計算ができるようになってほしいのですが、学校では計算の意味やブロック図や絵をかいて説明すること、考え方を重視しています。教科書でもそういう展開になっています。授業ではその部分を話し合いながら学習するのですが、最終的にはドリルなどで計算ができることが目標となってしまうため、意味や説明の学習がどこかに飛んで行ってしまいます。たし算では初めにこんなことがありました。
①きんぎょを男の子が3ひき、女の子が2ひきすいそうにいれると5ひきになります。
②きんぎょが5ひきはいっているすいそうに3ひきいれると8ひきになります。
この2つ、どちらもたし算ですが、意味や答えの出し方がちがいます。
教科書では、このような図になります。
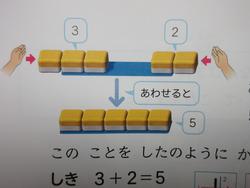
意味は違うのですが、どちらもたし算になります、と最後はまとめています。 つづく。
10月12日(月)
3年生が習いたての円を買ったばかりのきれいなコンパスでかいていました。


何度も消したり、ノートに大きな穴が開いたり、苦労しています。教科書には円のかき方とコツがかいてありますが、もう少し練習しないとスムーズにはかけないようですね。3年生、頑張れ。
左は使用している教科書です。 右は別の会社ですが、説明に1ページを使っています。
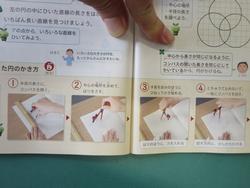
他の教科書会社もみてみましたが、ポイントをまとめると①回すときに自分の体まで鉛筆先を近づけてからスタートする。②回す方向に傾ける。③鉛筆と針の先を同じにする。ということが書いてありました。お子さんと一緒にぜひかいてみてください。慣れれば上手にスッとかけるようになります。
10月5日(月)
この土日にテレビでよく季節ごとにある新番組の番宣を兼ねたクイズ大会がありました。その中の問題で興味深い算数の問題がありました。小学校算数では有名な問題です。
Q この2つのうち答えが20になるのはどれ?
① 7+3×2 ②2+3×6 さあ5秒で考えましょう。
芸能人48人の出した答えは①26人②22人です。問題の数字ははっきり覚えていないのでちょっと作りましたが、人数はしっかり覚えています。さて、正解はどちらでしょう。
この問題は4年生の学習内容です。6年生が春に行う学力学習状況テストの算数の基本問題にもたびたび出されるような間違えやすい問題です。平成31年度と平成29年度はなんと同じ問題で 6+0.5×2 正答率は順に60.8%と66.8%です。これは小数も入っていました。さらにさかのぼって平成26年度は 100-20×4 、 平成22年度は 50+150×2 平成21年度は 80-30×5 正答率は順に81.1%と66.3%と67.0%でした。だいたい70%前後の全国の6年生の正答率と言えるでしょうか。
さあやっと答えです。答えは②ですね。①は13になります。芸能人は早く計算しないといけないので、つい前から7+3=10、10×2=20とやってしまったのですね。芸能人の正答率は45.8%になります。
4年生では計算のきまりでかけ算やわり算はたし算、ひき算よりも先に計算する。( )は何よりも先に計算すると学習します。これを忘れてしまうと6年生のこのような問題で間違えてしまうのです。それが小学生の場合は約3割いるということですね。5年生以上のお子さんにぜひ出してみてください。中学生以上のお子さんにも。
9月19日(土)
3年生筆算の続きからになります。まず、筆算はやり方を覚える前に、筆算の意味を知る、つまり、筆算を自分たちで作る学習が必要になります。23×3という習っていない計算を前回は20×3と3×3という今まで習った形に分けて答えを出しました。 次は何をすると思うと聞くと、「もっと大きい数」「わり算」「筆算」など思いつくままに子どもたちは発言します。「そう、次は筆算を考えます。」「今まで筆算はやったの。」と聞くと「やりました。」「たし算の筆算」「ひき算の筆算もやった」などが出てきます。そこで、「どうやったの。」で
23 23 ではかけ算も同じに考えれば 23 だね。
+ 3 - 3 × 3
ここで面白いのは、さらにたし算とひき算は1の位から位ごとに計算したことを確認して、かけ算の筆算をどうするか考えると、かけ算の筆算を考えた子どもたちの今回は40%ぐらいが答えを29と出すのです。なぜだかわかりますか。よく子どもたちに言うことは、間違った答えでもその原因がわかるかが大切、原因がわかれば正解になるし、間違えやすいポイントもわかる、間違えは大切なんです。この場合もまさにそれで、原因は今までと同じように1の位をかけただけだからです。
前の日に答えは69とやって、知っているはずなのに29となってしまうのです。これを、昨日学習した分けるやり方と比べて考えることにより、かけ算の筆算は3×3と2×3(実は20×3)を計算してたすという筆算の意味を理解したうえで、筆算のやり方も学習することになります。ただ、こういう意味の学習は必ずやるのですが、最後は計算練習の連続になってしまうので、結構忘れられてしまうのです。それが悩みです。代表的なものにかけ算九九や面積の公式があります。これらも意味をしっかり考えて学習するのですが、最終的には九九を覚え、公式を覚えとなってしまいます。考える楽しさをぜひ授業の中で体験してもらいたいです。

9月14日(月)
3年生の算数の続きです。隣のクラスは先週ちょうどかけ算の筆算に入るところでした。かけ算九九から、20×3を学習し、23×3に入り、23×3の筆算を学習するあたりです。
算数の授業は基本的には習ったことをもとに習っていないことを解決します。20×3は習っていませんが、10のまとまりで考えて2×3にします。よく使われるのは10円玉です。10円玉で考えると20円は10円玉が2個、それが3セットで2×3=6、この6は実は10円玉が6個なので60円となります。100円玉で考えれば300×3は3×3になります。
では23×3はどのように習った形にするのでしょう。それは23を20と3に分けるのです。そうすれば23×3は20×3と3×3という習った形の和になります。これを授業では図や式を使って説明します。よって60+9=69になります。
実はこの考え方は1年生から学習しています。1桁のたし算(1~9まで)しか知らない1年生は10+2を学習し、続いて20+30を学習します。10+2ならブロックでできますが、数が大きくなると大変です。ここで10のまとまりで考えると、20+30は2+3になるのです。この考え方は小数や分数でも使われます。何度でも登場するお決まりの考え方です。
さらに、分けるという考え方は2年生のかけ算の学習でも使っています。1~5の段を学習した後、6~9の段の答えを探す学習に入ります。かけ算九九は覚えるだけの学習ではありません。その前にかけ算九九を作り出す活動があります。この活動によってかけ算九九の意味や構成を学習します。
6の段の答えを求めるときには、2の段と4の段に分ければできるという考え方。つまり、6×3は2×3と4×3に分ければ、6+12で18、と習ったかけ算九九で習っていない6の段の答えを見つけることができるということです。これはその後13×5など大きい数のかけ算にも使われる考え方です。 筆算につづく。
9月8日(火)
先週3年生の算数の時間を見学しました。かけ算の筆算を学習していました。繰り上がりのある筆算を考えていたのですが、どの子もやり方はわかっているようでした。かけ算九九がちょっと心配な子もいて、九九の復習も必要だなと感じました。そういう子はかけ算九九さえわかれば、筆算ができるのです。かけ算九九を何とかしたい。と考えていたら、ふとかけ算九九の歌はないのかなと。20年以上前に「ロックンロール県庁所在地」という歌があって、歌で覚えるのは一つの方法だなと思いましたが、ネットで調べてみるとドラえもんなんかも出ていましたが、あまりよさそうなものがありませんでした。ひたすら唱えるしかないでしょうか。特に間違えやすい段を学校の行き帰りやお風呂などで口ずさむとよいのですが。一つの段ならあっという間です。家庭でも確認を。特に危ないのは6~8の段です。下の段では3×7、4×7あたりでしょうか。
8月25日(火)
前回の分数÷分数はなぜわる数の逆数をかけるのか、についての話をします。教科書では図や計算のきまりを使って説明しています。私が好きな方法は計算のきまりを使って、わる数を1にする方法です。わる数が1になればわらなくても同じです。つまり、3÷1=3です。分数で考えてみると、例えば2/5÷3/4ではどうなるか。わる数3/4を1にするためには3/4の逆数4/3をかければよいですね。3/4×4/3=1です。ここで計算のきまりを使うとわる数に4/3をかけたのだから、わられる数にも同じ数4/3をかけなければいけません。例えば6÷2は(6×2)÷(2×2)です。同じ数2を両方にかけても答えは変わりません。
分数に戻りますと、4/3を両方にかけるので、2/5÷3/4=(2/5×4/3)÷(3/4×4/3)になります。そして(3/4×4/3)=1なので、2/5÷3/4=(2/5×4/3)÷1になります。÷1はなくても同じなので、最終的には2/5÷3/4=2/5×4/3となり、逆数をかけているということになります。
ちょっと字ばかりで読みたくなくなってしまいますが、どうでしょうか。今はネットをみれば何でも調べられるので、この分数÷分数もネットで検索すれば動画で解説しているものがたくさんあります。かなりわかりやすいと思います。5~10分程度です。興味があればぜひ。
8月18日(火)
6年生の1学期は分数のかけ算わり算の学習がありました。分数と聞くと「あ~面倒くさい」となりがちですが、5年生で学習する分数のたし算ひき算に比べると、やややさしい?5年生では分母を同じにしないと(通分をしないと)計算ができないので、これがややこしい一つの原因です。1/2+1/3=2/5とできればいいのですが、実際には分母を6に通分して3/6+2/6=5/6ですね。これに対して6年生のかけ算わり算は、かけて約分するだけなので(わり算もかけ算にしますね。)結構簡単なのです。
ただここで一つ大切なことがあります。「なぜ、分数のわり算はわる数を逆数にしてかけるのか。」ある教員養成系の大学教授が学生にこの問題を出したところ、2割も正解がなかったという話をずいぶん昔に聞きました。学生としては小学校で「逆数にしてかければよい。」と習ったのだから、何の疑問も持たず計算をしていたとのこと。計算はできるが、それがなぜできるのかという意味が不十分だということです。代表的なものは、たとえば面積の公式も三角形、台形、円など、公式は言えるけどなぜあの公式ができたのか、という公式を作る授業があります。小学校の教科書ではその意味について学習はするのですが、どうしてもそのあとに問題を解く必要があるので、意味はどこかに忘れ去られ、やり方だけが頭に残るというのが現状ではないでしょうか。続きは次回へ。
8月17日(月)
4年生の1学期の算数のポイントと言えば、初めて出てきた小数とわり算の筆算ではないでしょうか。ここではわり算の筆算を取り上げます。3年生ではかけ算九九で解けるわり算でしたが、4年では割られる数が2桁、3桁になります。そしてそれを簡単に解くために筆算を学習します。
算数では新しく出てきた計算は習った計算にすることができれば、簡単に解くことができる。が基本になります。ここではまず80÷4,600÷3が出てきますが、いずれも10,100のまとまりで考えれば8÷4、6÷3という習った計算になり、簡単に解けるとこになります。
次は72÷3が出てきます。これは72を60と12に分ければ、60÷3=20と12÷3=4で合わせて24とできます。この考え方を図を使って表す(P42)と筆算(P43)ができあがります。筆算は形を覚えるものではなく、どのようにしてその筆算ができたのかを授業ではまず考えます。でも実際には筆算が使えるように何度も練習しますので、最後はやり方を覚えること(たてる、かける、ひく、おろす)が中心になってしまいますが、なぜそうなるかを学習することはとても大切なことです。
その後、あまりや3桁÷1桁が出てきますが、筆算の意味を図と見比べながら考えていきます。2学期はこれを元にして、最大の難関(だと私は思っています。)÷2桁が出てきます。(たとえば86÷23)あと1週間ほどで授業が再開されますが、この1桁でわるわり算の復習を十分にやってほしいと思います。そして÷2桁を理解してほしいと思います。
なぜ、最大の難関? わり算は実はわり算といっていますが、たとえば72÷3を解くには、
7÷2=3あまり1、2×3=6、7-6=1、1を10として10+2=12、12÷3=4と÷、×、-、+となんと全部の計算が入っているのです。それをすべて正確に解きます。これは大変なことです。さらに、2学期の2桁で割るわり算には、見積もりや予想が入ってきます。これがまたやっかいです。前出の86÷23であれば答えは3なのか4なのか迷います。予想が違っていれば考え直します。これは本当に大変です。この学習の時は是非お子さんのノートを見て、応援をしてあげてください。
8月6日(木)
前回途中だったところを補足します。30というのは、十の位が3、一の位が0、または10が3個、さらに6×5、50-20、29の次などいろいろな見方があります。算数では「相対的な」見方、相対的な大きさなどといいますが、これは数の仕組みを理解し、数の感覚を豊かにするために大切な要素です。1年生では今学期に20まで、3学期には100まで、そして2年生では1学期に1000まで、3学期には10000まで、4年生では億や兆、そして小数、分数と範囲を広げながら学習します。数直線で表したり、位の数を考えたり、10が何個で考えたり、あといくつで○○などいろいろな問題が出てきます。今学期は2年生で100より大きい数、4年生で小数のしくみを学びました。きっとわかりづらいところだと思いますので、eライブラリーなどで復習をしてほしいと思います。
チェック問題 2年 ①430は10が何個? ②1000より70小さい数は?
4年 ①30.5を1/10した数は? ②3.2は0.01を何個集めた数?
どうでしょう。4年の問題なら5,6年生にも聞いてください。
3年生には、かけ算九九の復習もおすすめします。2年生後半あれだけやったかけ算九九も3年でサボっていると忘れる子が2割ほどいます。「6の段言ってみて」で調べてください。10秒でわかります。できなかったら、毎日少しでいいので唱えさせてください。3年の1学期「わり算」「あまりのあるわり算」2学期「大きな数のかけ算」でたくさん使います。経験から、忘れやすいのは6,7,8の段、3×7、4×7、あたりです。
(答え2年①43個②930、4年①3.05②320個)
8月4日(火)
7月に6年生の教室でちょっと興味を引かれたことがありました。黒板には「メイク10」と書かれていて、その下に数字が4つ、たしか、4,5,6,8。この4つの数字を使って10を作るという、ちょっとした頭の体操?私たちもその昔、切符の数字や車のナンバーの4つの数字を使って作ったのでは。それを算数のはじめの時間にやっていました。1分ほど考えてみましょうか。答えはのちほど。
さて、私も実はこの学校に来て、あるものがなかったのでさっそく10個買ったものがあります。

やり方は黒い数字の十の位と一の位の合計の数字(ここでは30と4で34)に、白の5つの数字(1~6まで、ここでは2,3,3,5,6)を+-×÷をして黒の数字の合計に合わせます。メイク10より複雑ですね。数字が多い分、難しくなりますが数が作りやすくなります。少しやってみましょう。答えは何通りかある場合とないときもあります。答えはこれまたのちほど。
このジャマイカのやり方は、6,7月に4年生以上のクラスを全部回って紹介してきました。興味を持ってくれた子もだいぶいたようで、その後、クラスに貸し出しもしました。ただ、コロナのためみんなで触って自由にやってみようは言えないところが残念でした。2学期にはジャマイカの大会を開きたいと考えています。
メイク10もそうですが、ここでは数字の見方・考え方が必要になってきます。10であれば2×5とみるか、60÷6とみるか、34であれば、30+4とみるか、17×2とみるか、+-か、×÷か、という数字の見方が必要になるのです。
実はこの考え方のもとは1学期の学習でも出てきました。それは次回に紹介するとして、答えを。
メイク10は、(4+6-8)×5=10、(4+8)×5÷6=10 … 子どもたちは5つぐらい出していました。
34は、(3+3+5+6)×2、5×6+3+3-2 まだあるでしょうか。
最後に、6年生に教えた2,3日後女の子が来て、先生、「私アマゾンで買ったよ。」と。わたしはとてもびっくりしました。今まで、かなり紹介してきましたが、まさか買ってしまうとは、これは初めてです。